Extra dimenziók: kicsi, nagy, vagy végtelen nagy?
Hogyan változott az elmúlt három évben a lehetséges gravitációs elméletekrõl kialakított felfogásunk? Ezt mutatjuk be az extra dimenziókról szóló írásunkban. Ez idõ alatt nyilvánvalóvá vált; lehetséges, hogy az általunk tapasztalt Newton-féle gravitációs állandó nem alapvetõ természeti állandó, csak egy (nagy távolságokra érvényes) effektív paraméter. Az ilyen elméletekben, amint bizonyos energiaskála fölé jutunk, extra dimenziók nyílnak meg elõttünk, ahol a gravitációs vonzástörvény eltér a hagyományos newtoni gravitációtól. A megdöbbentõ újdonság ezekben az új elméletekben az, hogy az energiaskála, ahol az extra dimenziók megnyílnak, egészen közel lehet a jelenleg kísérletileg elérhetõ energiákhoz, és az extra dimenziók hatásai az elkövetkezõ generációs gyorsítókban esetleg kísérletileg ellenõrizhetõk lesznek.
Az
egyik legalapvetõbb és legrégebbi fizikai törvényünk
a Newton-féle gravitációs kölcsönhatás,
ami szerint két (m1 és m2 tömegû)
test között fellépõ gravitációs
erõ nagysága
| F(r) = GN ·m1m2/r2 , | (1) |
ahol GN a Newton-féle gravitációs állandó, r pedig a két test közötti távolság. Ez az egyenlet igen jól magyarázza a bolygók Nap körüli mozgását, a rakéták pályáját stb. A gravitációs állandót az úgynevezett Cavendish-féle kísérlettel lehet mérni, amely során a két test között fellépõ erõt nagy precizitással mérjük. Ezen mérések szerint a gravitációs állandó értéke
GN = 6,67 ·10–11 m3/kgs2.
Hosszú idõ telt el, amíg a Newton-féle erõtörvény eredetére fény derült. Einstein 1915-ben alkotta meg gravitációs elméletét, az általánosrelativitáselméletet. Ennek alapja az, hogy a tömeggel rendelkezõ testek magát a téridõt görbítik el, és a testek gravitációs gyorsulását a görbült térben való egyenes vonalú egyenletes (geodetikus) mozgás okozza. Az Einstein-elméletbõl következik a Newton-féle gravitációs törvény gyenge terek esetén. Az Einstein-féle gravitációs elmélet alapvetõ mennyisége az úgynevezett metrikus tenzor gmn (x), ami a téridõ geometriáját írja le. Az indexek értéke m, n = 0, 1, 2, 3, x0 = t az idõkoordinátát jelenti, x1, 2, 3 pedig a térbeli koordinátákat. Az általános relativitáselmélet egyetlen állandója szintén a Newton-féle gravitációs állandó. Sokkal célszerûbb azonban a gravitációs állandó helyett bevezetni a vele ekvivalens tömegskálát, GN=h–c/MP2, ahol MP a Plank-tömeg (Planck-skála). Ez azért célravezetõ, mert ennek a tömegskálának valós fizikai jelentése van: ez olyan energia, amit elérve a gravitációs kölcsönhatás erõssége összemérhetõvé válik a többi (erõs, gyenge és elektromágneses) kölcsönhatáséval. Szintén ez az az energiaskála, ahol a gravitációs kölcsönhatás maga is erõssé kezd válni. Erre abból lehet következtetni, hogy az egyes gravitációs folyamatokhoz járuló kvantummechanikai korrekciók (hurokkorrekciók) ezen energiaskálán kezdenek jelentõssé válni. Vagyis ez az a skála, ahol a gravitáció kvantumelmélete fontossá válik, és a klasszikus közelítés (ami Einstein általános relativitáselmélete) már nem alkalmazható többé. Részecskefizikai egységekben kifejezve MP» 1019 GeV, vagyis kb. 1019-szer nagyobb a proton tömegénél, és 1017-szer a gyenge kölcsönhatás alapvetõ skálájánál!
A hierarchia probléma
Négy különbözõ alapvetõ kölcsönhatást ismerünk, amelyek az elemi részecskék között felléphetnek: az elektromágneses kölcsönhatást, ami igen nagy szerepet játszik hétköznapjainkban, a gyengekölcsönhatást, amely a neutron úgynevezett b-bomlásáért felelõs, az erõs kölcsönhatást, ez tartja egyben az atommagot, és természetesen a gravitációt, ami a részecskék tömegével arányos vonzóerõt ad. Az elmúlt harminc évben kiderült, hogy az elektromágnességet és a gyenge kölcsönhatásokat egyetlen egyesített elmélettel lehet leírni, ez az elektrogyenge-elmélet (más néven a Standard Modell). Ennek alapvetõ energiaskáláját a kölcsönhatást közvetítõ részecskék (W- és Z-mértékbozonok) tömege határozza meg, és értéke hozzávetõlegesen 100 GeV, vagyis a proton tömegének 100-szorosa. Ezen kívül az is világossá vált, hogy az erõs kölcsönhatás is igen jól beilleszthetõ a Standard Modellbe, ha az erõs kölcsönhatás kvarkok között hat, amely kvarkok a proton és a neutron elemi építõkövei. Tehát az elektrogyenge és az erõs kölcsönhatások egyetlen egyesített elmélettel, a részecskefizika Standard Modelljével írhatók le, és az elmélet alapvetõ elemi skálája 100 GeV körüli. Láttuk ellenben, hogy a gravitációs elmélet skálája ennek a 1017-szerese (ami azt mutatja, hogy a gravitációs kölcsönhatás elemi részecskék között jóval gyengébb, mint a másik három erõ).
A gravitációs skála hatalmas értéke okozza a részecskefizika egyik legnagyobb dilemmáját: hogyan lehetséges, hogy a két elmélet (amelyek remélhetõleg egyetlen alapvetõ elmélet két különbözõ megnyilvánulásai) skálája ilyen mértékben különbözzön egymástól. A kvantumelméleti effektusok (hurokkorrekciók) még súlyosabbá teszik ezt a problémát: a Standard Modellben ugyanis létezik egy (mindmáig kísérletileg nem észlelt) részecske, a Higgs-bozon, ami alapvetõ szerepet játszik az elméletben, hiszen az öszszes többi részecske a Higgs-bozonnal való kölcsönhatás révén „kap” tömeget. Tehát ennek a Higgs-bozonnak a tömege és a kölcsönhatásai határozzák meg a modell összes többi részecskéjének a tömegét. A kvantumeffektusok (hurokeffektusok) révén viszont a Higgs-bozon tömege MP nagyságú korrekciókat kapna. Vagyis a Standard Modellben az elektrogyenge-elmélet skálája destabilizálódik a kvantumeffektusok révén, és ez a gravitációs kölcsönhatás Planck-skálája és az elektrogyenge-skála közti óriási különbség következménye. Ezt nevezik hierarchia problémának, ami a részecskefizika egyik legmélyrehatóbb kérdése. Az elmúlt két év új extra dimenziós elméleteinek egyik fõ célja, hogy magyarázatot találjanak erre az izgalmas kérdésre.
Extra dimenziók
Kaluza és Klein már az 1920-as években felvetette, hogy az általunk érzékelt négy téridõ-dimenzió mellett létezhetnek még extra dimenziók is. Ez az ötlet elõször azért vetõdött fel, mert ez lehetõséget nyújtott az elektromágnesség és a gravitáció egyesítésére. Bár ez a kísérlet akkor nem járt sikerrel, az extra dimenziós elméleteket azóta is Kaluza–Klein–elméleteknek nevezik. Az elmúlt húsz évben a fizikusok egyre komolyabban veszik azt a lehetõséget, hogy extra dimenziók ténylegesen léteznek. Az alapvetõ motiváció a húrelméletbõl származik. A húrelméletben az alapvetõ részecskék szerepét egy apró rezgõ húr veszi át. Ez a hipotézis azért izgalmas, mert a húr elemi gerjesztései (amelyek az elemi részecskéknek felelnek meg) automatikusan tartalmazzák a gravitáció kvantumát, a 2-es spinû gravitont. A húrelmélet egy véges kvantumelmélet. Ez az egyetlen olyan ismert elképzelés, aminek kereteiben a gravitációnak egy konzisztens kvantummechanikai leírása adható. Viszont kiderül, hogy maga a húrelmélet csak tíz (vagy az ún. „M-elméletben” tizenegy) téridõ dimenzió esetén lehet konzisztens. Vagyis a húrelmélet hat (vagy esetleg hét) valós fizikai extra dimenziót jósol.
Hogyan lehetséges, hogy nem érzékeljük ezeket a dimenziókat? A legkézenfekvõbb magyarázat az, hogy e dimenziók kvalitatíve különböznek a mi közönséges négy téridõ-dimenzióinktól: a megfigyelt téridõ-dimenziók végtelen kiterjedésûek, míg az extra dimenziók kompaktak (végesek). Amennyiben e dimenziók mérete kicsi, nem érzékeljük õket (1. ábra).
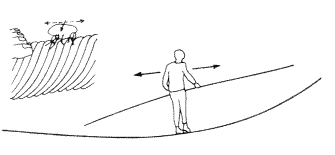
1. ábra. A kötéltáncos
úgy érzi, hogy csak egy irányba tud mozogni
a kötélen: elõre vagy hátra, mivel a kötél
sugara sokkal kisebb teste paramétereinél. A kötélen
a bolha viszont körbe tudja szaladni a kötelet, két
irányba tud mozogni: a kötél mentén és
körbe a kötélen, mivel mérete összemérhetõ
a kötél (vagyis az extra dimenzió) méretével.
A
fizikusok hosszú ideig úgy tartották, hogy a
kompaktdimenziók mérete csak irtózatosan kicsi,
r » 1/MP » 10–33 cm nagyságú
lehet. Hogy megértsük, miért tartotta magát
ez a felfogás hosszú évekig, el kell magyaráznunk,
mi az összefüggés a teljes extra dimenziós
elmélet és az általunk észlelt effektív
négydimenziós elmélet paraméterei között.
Megmutatható, hogy az általunk észlelt Planck-skála
(ami ekvivalens a gravitációs állandóval)
a következõ egyszerû összefüggéssel
fejezhetõ ki:
| MP2 = M*n+2 · rn, | (2) |
ahol
M* a teljes 4+n dimenziós elmélet Planck-skálája
(amely a valódi fundamentális skálája
az elméletnek), r az extra dimenziók mérete,
és n az extra kompaktdimenziók számát
jelenti. Vagyis az extra dimenziók térfogata, V=rn
jelenik meg a paraméterek közötti illesztést
meghatározó egyenletben. Hasonló módon
megmutatható, hogy az extra dimenziós elmélet
és az általunk észlelt effektív négydimenziós
elmélet csatolási állandói közötti
összefüggés a
| g2 = g*2/V | (3) |
képlettel
adható meg, ahol g* az extra dimenziós elmélet
csatolási állandója, míg g ugyanez
a négydimenziós elméletben. Mivel azt szeretnék,
hogy g*2 ne legyen túl nagy (Planck-skálákban
mérve), ezért feltételezték, hogy V=rn»
M*n, vagyis MP» M* » 1/r, tehát
az extra dimenziók hihetetlenül kicsinyek, és a
hatásuk belátható idõn belül nem
mérhetõ semmilyen kísérlettel.
Az új ötlet: brane-ek extra dimenzióban és nagy extra dimenziók
1998-ban Arkani-Hamed, Dimopoulos és Dvali (ADD) felismerte, hogy az elõbbi érvelés alapvetõen azon a feltételezésen nyugszik, hogy az alapvetõ extra dimenziós elmélet csatolási állandója ne legyen túl nagy, vagyis g*2 = O(1). Az elmúlt öt évben azonban megértettük, mind a térelméletekben, mind a húrelméletben szükségszerûen léteznek kiterjedt objektumok (szolitonok), amik egy membránhoz hasonlítanak, azzal a különbséggel, hogy térszerû kiterjedésük esetleg nem kétdimenziós. Ezeket az objektumokat a membrán szó angol megfelelõjébõl brane-eknek nevezik. Ezek alapján a membránt 2-brane-nek hívjuk (hisz két térszerû dimenziója van), a húrt 1-brane-nek stb. Számunkra a legérdekesebb objektum a 3-brane, hiszen ennek éppen három térszerû dimenziója van, ugyanúgy, mint az általunk fizikailag érzékelhetõ dimenziók számának.
Arkani-Hamed, Dimopoulos és Dvali megdöbbentõ javaslata az volt, hogy mi (és velünk együtt az Standard Modell összes tere) a 3-brane-hez rögzített, és nem tudunk arról elmozdulni (akárcsak egy hangya, ami kötélen mászik, lásd a 2. ábrát). A gravitáció azonban maga a tér deformációja, tehát a gravitáció szükségszerûen az összes téridõ dimenzióban terjed. Amennyiben a SM-terek tényleg a 3-brane-hez lokalizáltak, akkor a g* csatolási állandóra nem kell semmiféle illesztési feltételt kiróni (hiszen a mértékelmélet háromdimenziós) és csak a gravitációs paramétereket kell illeszteni a (2) egyenlet segítségével. Ekkor viszont nincs semmiféle elv, amely szerint M* » MP, és az extra dimenziók nagysága sokkal nagyobb is lehet 1/MP-nál. Ebben az esetben a megfigyelt gravitációs állandó (és a Planck-skála) nem valódi természeti állandó, csak egy effektív paraméter, amit a jelenleg elérhetõ energiákon mérünk. Amennyiben elég nagy energiákat (vagyis kis távolságokat) próbálnánk ki, akkor az extra dimenziók „megnyílnának” elõttünk, és a valós fundamentális természeti állandót, M*-ot mérhetnénk meg.
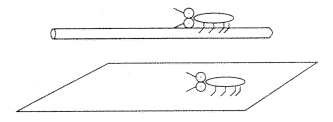
2. ábra. Mint ahogy a hangya nem tud elmozdulni a kötélrõl, a nagy extra dimenziós elméletekben mi magunk egy háromdimenziós brane-hez vagyunk rögzítve, amirõl nem tudunk elmozdulni az extra dimenziók irányába
Az egyetlen korlát M* nagyságára (jobban mondva kicsinységére) az, hogy az összes jelenlegi laboratóriumi kísérlet eredményét sikeresen reprodukáljuk. A helyzet az, hogy a Cavendish-féle kísérletet igen nehéz nagyon kicsi távolságokra elvégezni, jelenleg csak r ³ 1 mm távolságokra léteznek mérések. Hogyan korlátozza ez az extra dimenziók méretének a nagyságát? Amennyiben a tömegek távolsága jóval nagyobb az extra dimenziók méreténél, akkor (mivel a gravitációs fluxus nem tud kompakt dimenziókban elnyelõdni) az extra dimenziók hatása elhanyagolható, vagyis a közönséges négydimenziós Newton-törvényt látjuk. Ha viszont ennél kisebb távolságokra mérjük a gravitációs törvényt, akkor ilyen távolságokra az extra dimenziókban is kiterjed a gravitációs fluxus, és a gravitációs erõ nem 1/r2 lesz, hanem 1/rn+2. Mint említettük, a jelenlegi precíziós gravitációs mérések csak az r ³ 1 mm-t zárják ki. Vagyis elvileg elképzelhetõ, hogy akár 1 mm nagyságú extra dimenziók is létezhetnek, de mivel csak a gravitációs kölcsönhatás terjed az extra dimenzióban, nem érzékeljük az extra dimenziók hatását! Ezek után vizsgáljuk meg, milyen korlátot jelent a fundamentális elmélet gravitációs skálájára (M*-ra) az r ³ 1 mm » 10–3 eV feltétel. Két extra dimenzió esetén azt kapjuk, hogy M* ³ 1 TeV = 1000 GeV. Vagyis elképzelhetõ, hogy a fundamentális elmélet skálája nagyjából egybeesik az elektrogyenge elméletével. Ez azt jelentené, hogy automatikusan megoldódna a hierarchia probléma, méghozzá a lehetõ legegyszerûbb formában: a valós (fundamentális) skálákban nincs hierarchia, ez csak az effektív Planck-skálát vizsgálva tûnik nehézségnek. Amint megfelelõ nagy energiákra érünk, a valós M* Planck-skálát fogjuk megfigyelni. Mint említettük, n=2 extra dimenziónál M* = 1 TeV körülbelül 1 mm nagyságú extra dimenziót követel meg. Ez azt jelenti, hogy a hierarchia probléma ilyen jellegû megoldásánál a következõ precíziós rövid hatótávolságú mérések jelentõs eltérést kellene, hogy mutassanak a Newton-törvényben, F » 1/r2 helyett 1/r4-t kellene mérniük!
Amennyiben több mint két extra dimenziónk van, és továbbra is azt akarjuk, hogy M*=1 TeV legyen, akkor az extra dimenziók mérete rn=3=10–7 cm, rn=4=10–10 cm, rn=5=10–11 cm, ..., rn®¥ = 1/TeV = 10–17 cm.
Vagyis látható, hogy ezekben az elméletekben az extra dimenziók mérete mindig jóval nagyobb, mint 1/MP, és a kísérletileg megengedett legnagyobb érték n=2 esetén lép fel.
Ezért ezeket az elméleteket „nagy extra dimenziós elméleteknek” hívjuk, gyakran szubmilliméteres extra dimenziós elméleteknek is nevezik õket. A fenti számértékekbõl látszik, n>2 esetén nem valószínû, hogy a gravitációs kísérletek a közeljövõben jelentõs eltérést mutatnának a Newton-törvénytõl.
Görbült extra dimenziók
Az
eddig ismertetett elméletek azt feltételezték,
hogy az extra dimenziók geometriája triviális,
vagyis hogy nincs jelentõs görbület az extra dimenziók
mentén. Randall és Sundrum (RS) azonban
azt mutatták meg, hogy az extra dimenziós görbület
bevezetésével még izgalmasabb elméleteket
lehet találni. Randall és Sundrum modelljéhez
csak egy extra dimenzió szükséges, de be kell vezetni
egy negatív ötdimenziós L kozmológiai konstanst
is (L<0). Az ilyen kozmológiai állandó létezésének
lehetõségét elõször Einstein
vetette fel a kozmológiai tágulás problémájának
megoldására, de késõbb sokáig úgy
tûnt, hogy az állandó értéke nulla.
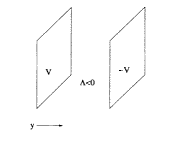
Emellett az ötdimenziós kozmológiai konstans mellett
a Randall–Sundrum-modellben szükséges egy pozitív
V>0 energiájú 3-brane, valamint ettõl nagyon
kis (r/s 1/MP) távolságra egy másik,
negatív (–V) energiájú brane (3. ábra).
Randall és Sundrum azt mutatták meg, hogy L és
V megfelelõ választása esetén az
Einstein-egyenleteknek létezik egy nagyon érdekes megoldása
(ún. ötdimenziós anti-de Sitter vagy AdS5
geometria), aminek fõ jellegzetessége, hogy a metrikus
tenzor exponenciálisan csökken a pozitív energiájú
brane-tõl távolodva az extra dimenzió mentén.
Ennek az exponenciális csökkenésnek az a következménye,
hogy a tömegskála változik az extra dimenzió
mentén:
| m(y) = m(0) e–ykr, | (4) |
ahol
r az extra dimenzió nagysága, y a pozitív
energiájú brane-tõl mért távolság,
k pedig egy L-tól függõ konstans. Vagyis,
ha éppen megfelelõ távolságra vagyunk
a pozitív energiájú brane-tõl, akkor elképzelhetõ,
hogy tömegskálánk automatikusan exponenciálisan
kisebb lesz, mint a fundamentális Planck-skála. Ez a
hierarchia probléma egy újabb igen elegáns megoldása.
 |
 |
| |
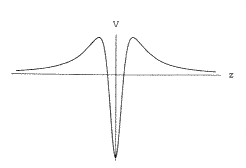
4. ábra. A gravitonok átlal érzékelt úgynevezett vulkán potenciál a Randall–Sundrum-elméletben. A „kráter” vonzóereje pontosan négydimenziós graviton kötött állapotot tesz lehetõvé, míg a kráter pereme kiszorítja a többi graviton módust a kráterbõl, és így effektíve négydimenziós gravitációt érzékelünk annak ellenére, hogy az extra dimenzió nem kompakt (hanem végtelen nagy). Ezt az effektust hívják a gravitáció lokalizálásának. Az ábrán a z koordináta az extra dimenzió irányát jelzi. |
Randall és Sundrum második javaslata az összes extra dimenziós elmélet közül a legmegdöbbentõbb: ha magán a pozitív energiájú brane-en élünk, akkor az extra dimenzió mérete akár végtelen nagy is lehet ebben az elrendezésben, és mégsem kerülünk ellentmondásba a Newton-törvénnyel! Ez azért van, mert a fentebb vázolt görbült térben (AdS5 térben) a gravitonok terjedése igen érdekes. Kiderül, hogy az egyes KK-módusok (lásd a következõ fejezetet) terjedését egy egyszerû kvantummechanikai Schrödinger-egyenlet írja le a „vulkán potenciálban” (4. ábra). A kráter a pozitív energiájú brane helyén található. Ebben a potenciálban (a kráter miatt) pontosan egy kötött állapot van, amit a négydimenziós közönséges gravitonnal lehet azonosítani, ami Newton-féle 1/r2-es gravitációs erõt okoz két próbatest között. A vulkán pereme viszont azt okozza, hogy a többi KK-módus kiszorul a vulkán kráterébõl, és így csak igen kicsi korrekciót fognak a Newton-törvényhez szolgáltatni. Ilyen módon magát a gravitációt is lokalizálni lehet egy brane-hez, aminek az a fantasztikusan hangzó következménye van, hogy létezhetnek akár végtelenül nagy extra dimenziók is, és mi mégis egy effekíve négydimenziós elméletet érzékelünk!
Kísérleti ellenõrzés az LHC-ben?
Az
eddigiekbõl látható, hogy igen érdekes
új extra dimenziós elméletek születtek az
elmúlt három évben. Amellett, hogy ezen elméletek
új alapokra helyezhetik a téridõrõl alkotott
alapvetõ felfogásunkat, talán a legfontosabb
tulajdonságuk ezen elméleteknek az, hogy (a hagyományos
húrelméleti modellekkel ellentétben) belátható
idõn belül kísérletileg is ellenõrizhetõk
lesznek. Itt most röviden áttekintjük az ismertetett
elméletek alapvetõ kísérleti következményeit.
Nagy extra dimenziók esetén két különbözõ
lehetõség áll fenn: n=2 extra dimenziónál
a precíziós gravitációs méréseknek
azt a megdöbbentõ eredményt kellene szolgáltatniuk,
hogy r<1 mm hatótávolság esetén a Newton-féle
gravitációs vonzóerõ nem 1/r2-tel
arányos, hanem 1/r4-nel! Amennyiben több mint
két nagy extra dimenzió létezik, a gravitációs
kísérletek valószínûleg nem mutatnak
eltérést a Newton-törvénytõl. Hogyan
lehetne akkor mégis tesztelni ezeket az elméleteket?
A kulcsot ehhez a kompaktifikáció részecskefizikai
következményeinek vizsgálata adja. Egy extra dimenziós
elméletben a gravitont feltétlenül egy 4+n dimenzióban
terjedõ térrel kell leírnunk. Ennek az a következménye,
hogy a tér azon állapotai, amelyek az extra dimenziók
mentén terjednek, négydimenziós szempontból
tömeges részecskéknek tûnnek. Egyszerû
példaként vizsgáljunk meg egy j(xi,
y) skalárteret öt dimenzióban, ahol az extra kompaktdimenzió
koordinátáját y-nal jelöltük.
Mivel az extra dimenzió kompakt, ezért a teret ki lehet
fejteni saját módusok szerint1.
Ez az ún. Fourier-féle móduskifejtés,
amely minden periodikus függvényre elvégezhetõ.
Mivel az extra dimenzió kompakt, ezért a teret leíró
függvény szükségszerûen periodikus az
extra koordinátákban. A Fourier-kifejtés ebben
az esetben a következõ alakban adható meg:
| (5) |
ahol pn = 2pn/r, n = 0, 1, 2, …
Ha a j tér öt dimenzióban tömeg nélküli, vagyis rá nézve p2=0, akkor a négydimenziós effektív jn módusok p2 = mn2 = (2pn/r)2-nek tesznek eleget, vagyis az extra dimenziós momentum négy dimenzióban tömegnek felel meg. Ez az úgynevezett Kaluza–Klein-kifejtés, és a jn tereket a j tér KK-módusainak („KK-torony”-nak) hívjuk. Ezen módusok tömege n=2 esetén n · 10–3 eV. Mivel gravitációs állapotokról van szó, a Standard Modell tereihez csatolásuk 1/MP-kal arányos, vagyis igen kicsi. Emiatt az egyes KK-módusok önmagukban nem okoznak mérhetõ effektusokat, viszont figyelembe kell venni, hogy a TeV energiák alatt hatalmas számú KK-módus helyezkedik el! A részletes számítások azt mutatják, ezen KK-módusok kollektív hatása a genfi CERN kutatóközpontban építés alatt lévõ LHC (Large Hadron Collider) kísérleteiben jelentõs mérhetõ effektusokat okoznak, vagyis a nagy extra dimenziós elméletek tesztelhetõek lesznek az LHC-ben! A legszembetûnõbb hatás az lehetne, hogy a nagyenergiás ütközés során egy ilyen KK-módust keltünk. Ennek a módusnak az impulzusa nem a mi négy dimenziónkba esik, vagyis ez a részecske elhagyná a mi brane-ünket. Ennek az a megdöbbentõ kísérleti következménye lenne, hogy szemmel láthatólag sérül az energia és az impulzus megmaradásának a törvénye, mivel a KK-módus az energia egy részét elviszi az extra dimenzióba (az ötdimenziós impulzusnak nem kell megmaradnia, mivel a brane jelenléte sérti az ötdimenziós transzlációs szimmetriát, ezért a mi négydimenziós impulzusunk egy része eltûnhet az extra dimenzióban). Például az LHC gyorsítóban (ahol proton fog ütközni antiprotonnal) a legfontosabb ilyen folyamat a
q![]() ® g G
® g G
lenne,
ahol q,![]() az ütközõ
kvarkot és antikvarkot jelenti, míg g egy közönséges
gluon, ami azután tovább bomlik, G pedig a graviton
KK-módusa, amelyik a hiányzó energiát
és impulzust szolgáltatja. Az elektron-pozitron gyorsítóban
az analóg folyamat e+e–®g G lenne,
ahol g egy virtuális foton, ami azután tovább
bomlik. Másik lehetõség ezen elméletek
kísérleti kimutatására abból származik,
hogy a gravitoncsere újabb adalékot adhat egyes kölcsönhatásokhoz.
Például az a meghökkentõ eredmény
is lehetséges, hogy az e+ e– ® f
az ütközõ
kvarkot és antikvarkot jelenti, míg g egy közönséges
gluon, ami azután tovább bomlik, G pedig a graviton
KK-módusa, amelyik a hiányzó energiát
és impulzust szolgáltatja. Az elektron-pozitron gyorsítóban
az analóg folyamat e+e–®g G lenne,
ahol g egy virtuális foton, ami azután tovább
bomlik. Másik lehetõség ezen elméletek
kísérleti kimutatására abból származik,
hogy a gravitoncsere újabb adalékot adhat egyes kölcsönhatásokhoz.
Például az a meghökkentõ eredmény
is lehetséges, hogy az e+ e– ® f![]() folyamat (ahol f egy fermion) hatáskeresztmetszete egy
adott küszöbenergiát átlépve növekedni
kezd a graviton KK-módusai miatt.
folyamat (ahol f egy fermion) hatáskeresztmetszete egy
adott küszöbenergiát átlépve növekedni
kezd a graviton KK-módusai miatt.
Végül meg kell említeni a legfontosabb lehetséges kísérleti következményt: amennyiben a fundamentális Planck-skála ténylegesen 1 TeV nagyságrendbe esik, az LHC képes lehet arra, hogy alapvetõ elméleteket (például a húrelméletet vagy más kvantumgravitációs hipotézist) kísérletileg megvizsgáljon, ami fantasztikus elõrelépésre adna lehetõséget a „végsõ elmélet” megismerése felé.
A Randall–Sundrum-elméletben viszont a KK-módusok egészen más tulajdonságúak, mint a nagy extra dimenziós elméletben. Itt a KK-módusok tömege TeV nagyságrendû, vagyis jóval nagyobb, mint a nagy extra dimenziós elméletekben, viszont a csatolásuk nem 1/MP-vel arányos, hanem 1/TeV-vel, tehát sokkal erõsebb, mint a nagy extra dimenziós elméletben. Ennek az a következménye, hogy az LHC-ben nemcsak a KK-módusok kollektív hatása lesz mérhetõ, hanem a egyes módusok is. A nagyenergiás ütközésekben kísérleti hatásuk viszont nagyjából a nagy extra dimenziós modellekkel egyezik meg, vagyis a KK-módusok hatására ismét hiányzó energiát lehetne észlelni, illetve a KK-módus kicserélése rezonanciákat okozhat egyes folyamatok hatáskeresztmetszeteiben.
A cikkben leírtak alapján jól látható, hogy az extra dimenziók fizikája szédületesen gyorsan fejlõdõ és izgalmas új ága a részecskefizikának. Az elkövetkezõ néhány évben még igen sok meglepõ (és esetleg megdöbbentõ) eredmény várható ebben a témában, amelyek alapvetõen befolyásolhatják a téridõrõl és a világegyetemrõl alkotott képünket, amelyek esetleg teljesen újszerû kísérleti eredményeket szolgáltathatnak.
Irodalom
[1]
N. Arkani-Hamed, S. Dimopoulos és G. Dvali, „The Universe’s
Unseen Dimensions” Scientific American 2000. August.
[2] „Theorists and experimenters seek to learn
why gravity is so weak”, Physics Today 2000. September, 22. p.
1 Gyakran a Fourier-kifejtést sinus és cosinus függvények segítségével adjuk meg, ami ekvivalens a fenti kifejtéssel.