HIDAS PÁL
Gluonlabdák és egzotikus mezonok
A kvarkok „színes" kölcsönhatása
Az 1960-as években Murray Gell-Mann állította fel az azóta kísérletileg is igazolt kvarkmodellt. Eszerint a mezonok egy kvarkból és egy antikvarkból1, a barionok pedig három kvarkból tevõdnek össze. Az elektromágneses kölcsönhatásban az azonos (pozitív-pozitív, negatív-negatív) töltések taszítják, a különbözõek (pozitív-negatív) vonzzák egymást. Az erõs kölcsönhatás esetén ez a kép úgy módosul, hogy ebben háromféle „pozitív" töltés van, amiket három színnek nevezünk, szokásosan a piros, kék, zöld választással. Mindegyiknek megvan a maga „negatív" töltése, a három „antiszín". Bármely kvark lehet a három szín közül bármilyen színû, ill. antikvark bármilyen antiszínû.Egyszerûsítve a következõ módon tudjuk a színkölcsönhatás alaptípusait összefoglalni. Egy szín a saját antiszínével együtt (pl. piros-antipiros) semleges töltést ad, azaz „színtelen". Ugyanígy semleges, azaz színtelen állapotot kapunk, ha mindhárom színbõl veszünk egyet-egyet (piros-kék-zöld állapot).2 A szín-antiszín vonzás mellett a három szín együttese is vonzza egymást, ami újdonság az egyszerûbb elektromágneses jelenségekhez képest. E kétfajta vonzás, valamint ezek kombinációi vezetnek stabil (kötött) állapotokhoz. A szín-antiszín vonzás tartja össze a kvark-antikvark felépítésû mezonokat, a háromszín-vonzás a három kvark alkotta barionokat, a különféle kombinációk pedig az egzotikus mezonokat és barionokat. Az elektromágneses kölcsönhatást a fotonok közvetítik. Azerõs kölcsönhatást közvetítõ részecskéket gluonoknakhívjuk (glue = enyv, ragasztó). A kvarkok és antikvarkok kölcsönhatásait a kvantum-színdinamika gluoncserékkel írja le. A gluonok egy nagyon lényeges tekintetben különböznek a fotonoktól. A fotonok csak egyféle töltés-antitöltés típus kölcsönhatásait közvetítik, s a kölcsönhatás során a töltések nem változnak meg, nem történik töltéscsere. A kölcsönhatás abból áll, hogy az egyik töltés energiájának és impulzusának egy részét a foton átszállítja a másik töltéshez. A gluonok viszont háromféle szín-antiszín között közvetítenek és biztosítaniuk kell a színcserét is az energia- és impulzuscsere mellett. Ezért a gluonoknak maguknak is van színük, míg a foton nem szállít elektromos töltést, azaz elektromosan semleges. A gluonok színe azonban eltér a kvarkokétól, éppen azért, hogy közvetíteni tudjanak a különbözõ színek között. A gluonok „kétszínûek", pl. piros-antikék, kék-antizöld stb. A piros-antikék gluon antirészecskéje a kék-antipiros gluon.
A kvantum-színdinamika (quantum chromodynamics, QCD) kvark-gluon bezárási jelensége miatt minden makroszkopikusan megfigyelhetõ részecskének szín szempontból semlegesnek, azaz színtelennek kell lennie. A kvarkmodell eredeti feltételezése szerint a mezonok mindig kvark-antikvark párok, a barionok viszont mindig háromkvark állapotok. Ez azonban önkényes megszorítás, bár hosszú ideig a kísérletekbõl úgy tûnt, hogy ez a feltételezés igaz. A gluonok nem semleges volta miatt azonban õk is létrehozhatnak kötött állapotokat. Megfigyelhetõ, szabad részecskét akkor alkotnak, ha az össztöltésük semleges. Ilyen pedig lehetséges, pl. ha egy piros-antikék és egy kék-antipiros gluont választunk.
Egzotikus kombinációk
Az ilyen két gluonból álló részecskét gluonlabdánakhívjuk, és az ún. egzotikus mezonokközé soroljuk õket, megkülönböztetésül az ún. konvencionális, azaz kvark-antikvark-mezonoktól. Lehetséges színtelen részecskét összerakni egy kvarkból egy antikvarkból és egy gluonból (pl. piros kvark és antikék antikvark, valamint egy antipiros-kék gluon). Az ilyen részecskét hibrid mezonnak hívjuk, s ugyancsak az egzotikus mezonok közül való. További lehetõségek a teljesség igénye nélkül a két kvark-antikvark párból összerakott mezon molekula, a három kvarkból és egy gluonból álló hibrid barion, a három kvarkból és három antikvarkból álló barion molekula,a három gluonból álló, ugyancsak gluonlabdánakhívott mezon stb. Az elvi lehetõségek száma korlátlan.
Megkérdezhetjük, hogy mi a jelentõsége ezen egzotikus állapotok esetleges létezésének. Ez éppen az, hogy megtalálásuk teszteli a kvantum-színdinamikát, ami megjósolja ezeket az állapotokat. Ha nem sikerülne megtalálnunk õket, akkor az elmélet revízióra szorulna. Van azonban problémánk magával a jóslattal is. Az elmélet nagyon jól kidolgozott nagyenergiájú folyamatokra, ezek a szórásfolyamatok, ahol a hadronok és így a bennük levõ kvarkok egymáshoz képest nagy impulzussal és energiával ütköznek és szóródnak egymáson. Ilyen esetekben nagy energiájú, de kevés gluon cseréjével jár az erõs kölcsönhatás, ahol a perturbációszámítás módszerével sok jegyre pontos számítások végezhetõk. Nagy energiájú folyamatoknál azért van kis számú gluoncsere, mert az egymáshoz képest nagy energiával repülõ részecskék csak viszonylag rövid ideig tartózkodnak egymás közelében, s így csak rövid ideig képesek az egymás által kibocsátott gluonok „elfogására".
Nem tudjuk azonban pontosan leírni a kötött állapotok spektrumát, azaz nem tudjuk megmondani pontosan, hogy az egyes hadronok tömege mekkora. A kötött állapotban ugyanis végtelen hosszú ideig tartózkodnak egymás közelében a kölcsönható részecskék, s ezért végtelen számú gluon cseréjét kellene leírnunk. Vonatkozik ez a konvencionális (kvark-antikvark) és az egzotikus részecskékre is. Közelítõ módszerekkel sikerült azonban talán 20-30%-ra becsülhetõ hibán belül kiszámolni egyes spektrumokat. A legígéretesebbek az ún. rács-kvantumszíndinamikai számítások. Ez a hiba azonban nagyon megnehezíti az egzotikus részecskék azonosítását, amik könnyen elbújhatnak a konvencionális részecskék tengerében.A mezonok „családjai"
Nézzünk meg konkrétan néhány jelöltet a legkönnyebb egzotikus mezonok esetére. Eddig a két protontömeg alatti tömegû mezonokat sikerült a legjobban feltérképezni, ebben a tartományban csak a három legkönnyebb kvarkot (u, d, s) tartalmazó mezonok fordulnak elõ. Egy konvencionális kvarkantikvark mezon a három felsorolt kvarkíz esetén összesen 3·3=9 kombinációt tesz lehetõvé, ezekbõl hat különbözõ, három pedig azonos kvark(antikvark) ízt tartalmaz. Szemléletesen ábrázolhatjuk ezt a kilenc mezont, ha a hat ill. három említett mezont egy hatszög csúcsaihoz, ill. geometriai középpontjához rendeljük (1. ábra). Így egy „mezonkilenceshez",egy mezonnonetthezjutottunk. Ez a kilenc mezon teljesen azonos tömegû lenne, ha a három felhasznált kvark tömege megegyezne.
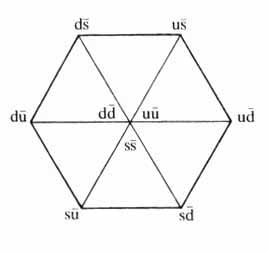
1. ábraEgy mezont azonban nemcsak az határoz meg, hogy milyen típusú kvarkok és antikvarkok vannak benne, hanem az is, hogy ezeknek milyen a relatív mozgása egymáshoz képest. Egy kvark-antikvark rendszer hasonlít egy hidrogénatomhoz, amiben az elektront kvarkra, a protont antikvarkra cseréljük. A kvark és antikvark egymáshoz képest számtalan héjon helyezkedhet el, amiket a relatív mozgásuk impulzusmomentumával, az ún. pályamomentummal különböztethetünk meg egymástól. Ennek értéke L = 0, 1, 2, 3,... lehet az impulzusmomentum legkisebb értékének (kvantumának) egységében mérve3. A kvarkoknak feles spinje, azaz saját impulzusmomentuma van, ezért a kvark-antikvark pár együttes spinje S=0,1 lehet, ellentétes ill. azonos irányú spinbeállás esetén. Amezon teljes J impulzusmomentumát a pályamomentum és a spin L+S kvantummechanikai összege adja. L=0 esetén J=S, L¹0 esetén pedig J = L-1, L, L+1 lehet. Ezen lehetõségek mind különbözõ mezonnonettekhez vezetnek, a lehetõségek száma határtalan, mivel az L pályamomentum (ésígy J is) tetszõleges egész szám lehet. Egy mezonnonettet a J,L, S kvantumszámok együttes megadásával jelölhetünk meg, az elfogadott spektrumjelölés szerint a 2S+1LJ alakban. Lszámértéke helyett szokásos az L = S, P, D, F,... jelölés is az L = 0, 1, 2, 3,... értékek helyett, ami analóg a hidrogénatom elektronhéjainak jelölésével.Az L és S kvantumszámokat kvantummechanikai elvi okok miatt kísérletileg sajnos nem tudjuk mérni, csak a teljes J impulzusmomentumot. Mérni tudjuk viszont a részecskék P paritását és C töltésparitását, mindkettõ +1 vagy -1 lehet. P a részecske tértükrözéssel szembeni, C a részecskék antirészecskéjükre való cseréjével szembeni viselkedését írja le. A P és C kvantumszámok az L és S kvantumszámoktól függenek, kvark-antikvark mezonok esetén P=(-1)L+1, C=(-1)L+S. A mezonokat így a 2S+1LJ kvantumszámok mellett a mérhetõ JPC kvantumszámokkal is jellemezhetjük. A kétféle címke oda-vissza nem egyértelmu, mert két 2S+1LJ címkéhez tartozhat ugyanaz a JPC címke. Így pl. a 2S+1LJ=3S1 és 3D1 mezonok egyaránt JPC=1-- kvantumszámokkal rendelkeznek. Hasonlóképpen a 2S+1LJ= 3P2 és 3F2 mezonok egyformán JPC=2++ részecskék.
Akik nem tartoznak "családokba"
Ha végignézzük, hogy az egyes L,S,J kvantumszámokból kvark-antikvark mezonok esetén milyen JPC kvantumszámok következnek, akkor kiderül, hogy a JPC=0--,0+-,1-+,2+-,3-+,... értékek nem lépnek fel. Azt mondjuk, hogy ezek tiltott kvantumszámok kvark-antikvark mezonok esetén. Ha mégis sikerülne ilyen kvantumszámokkal rendelkezõ mezont találni, akkor az biztosan nem kvark-antikvark, hanem egzotikus mezon, azaz gluonlabda, hibrid, vagy mezon- ill. barionmolekula lenne. Az egzotikus mezonok azonban nem feltétlenül rendelkeznek ilyen egzotikus kvantumszámokkal.
A részecskék kvantumszámai hosszadalmas analízissel, a bomlási módusaik feltérképezésével határozhatók meg a bomlástermékek kvantumszámai és térbeli szögeloszlása alapján. A növekvõ kvantumszámok általában növekvõ tömegû mezonnonettekhez vezetnek, a legkönnyebb az 1S0 nonett, ezt követi a 3S1, majd 1P1, 3P2, 3P1, 3P0 a sorrend. Bonyolítja a helyzetet, hogy minden részecskének lehetséges az N = 0, 1, 2, 3,... radiális kvantumszámnak4 megfelelõ gerjesztett állapota. Az általunk vizsgált tartományban ezek még nem nagy számban jelennek meg. A 2. ábra mutatja néhány nonett mezonjait. A zárójelben levõ szám az illetõ mezon tömege MeV/c2 egységben mérve.
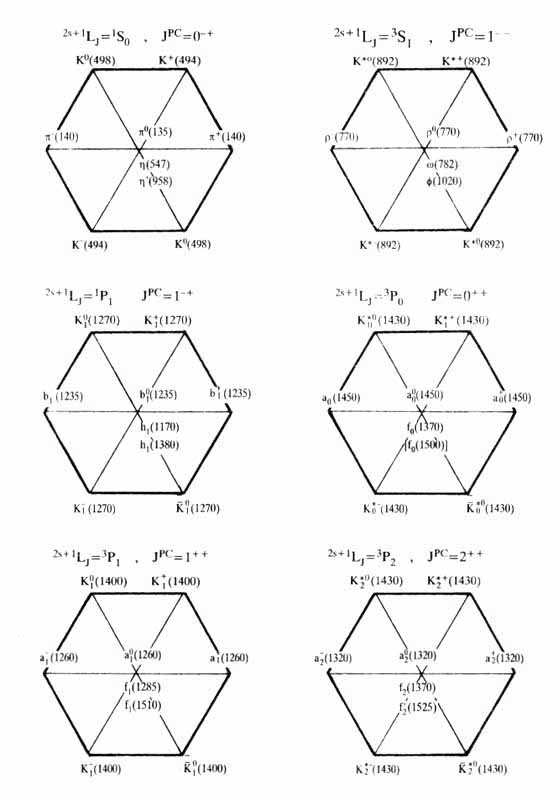
2. ábra. MezonnonettekA konvencionális mezonokat tehát nonettekbe csoportosíthatjuk és ezt kísérletileg is sikerült igazolni. Maradt azonban néhány olyan mezon, amit nem sikerült így besorolni, ezek a fõ egzotikus mezonjelöltek. A legkisebb tömegû négy ilyen részecske az f0(980) és a három a0(980), amik nem egzotikus, JPC=0++ kvantumszámúak. Az elõbbi semleges, az utóbbi viszont -1, 0, +1 elektromos töltésû lehet a pionokhoz hasonlóan. Az analízisek arra mutatnak, hogy ezek a részecskék valószínûleg KK mezonmolekulák, tömegük igen közel esik két kaon tömegének összegéhez.A 3P0(0++) nonett f0 mezonjai az elsõ gluonlabda jelölt szempontjából nagyon fontosak. Az elméleti (rács-kvantumszíndinamikai) számítások szerint ezek tömegének tartományába kell esnie a legkisebb tömegû gluonlabdának, aminek kvantumszámai éppen megegyeznek az itt található konvencionális mezonok kvantumszámaival. Ilyenkor egy sajátos kvantummechanikai jelenség, a részecskék keveredése léphet fel. A „kevert" részecske rendelkezik határozott tömeggel és élettartammal, az „eredeti komponensek" nem figyelhetõk meg. A keveredés valószínûsége annál nagyobb, minél közelebb esõ tömegekrõl van szó, és akár három részecske is keveredhet. Ilyen keveredés egyébként a konvencionális mezonok esetén is rendszeres a nonett közepén található két (a háromból) részecske között. Ilyen pl. az w-f keveredés vagy az h-h' keveredés. Ez a keveredés megváltoztatja a mezonok kvarktartalmát, pl. a f-mezon (3S1 nonett) lényegében csak s-kvarkot és antikvarkot tartalmaz, ami miatt elõszeretettel bomlik s-kvarkot tartalmazó (KK) részecskékre, az ilyet nem tartalmazó bomlás módusai (pl. pp, ppp, rp) erõsen el vannak nyomva.Egy gluonlabda, mivel nem tartalmaz semmilyen kvarkot, egyformán preferálja bármelyik kvark megjelenését a bomlási módusaiban. Ha viszont összekeveredik egy konvencionális mezonnal, akkor a bomlási módusokban a fénytanból ismert interferenciával rokon jelenség miatt elõfordulhat egy nagyon furcsa eset. Szokatlanul felerõsödhet egy bomlási módus, az egyszerû összeadásnál erõsebben - ezt konstruktív interferenciánakhívjuk -, de az ellenkezõje is megtörténhet. Bomolhat valamely módon a konvencionális mezon és a gluonlabda különkülön, a kettõjük turmixa viszont teljesen mentes lehet ettõl a módustól, amit destruktív interferenciánakhívunk. Ez a jelenség is igazolja a részecskék hullámtermészetét és a kvantummechanikai leírást, amiben a részecskék nem tömegpontok, hanem valószínûségi hullámfüggvények. Külön-külön a két hullámfüggvény reprezentálhat egy bomlási módust, de ha ellenkezõ (180°-os szöggel eltolt) a fázisuk, akkor kioltják egymást bizonyos bomlási módusokban. Analóg ez a fény interferenciájával. A tényleges valószínûségeket pedig a hullámfüggvények összegének abszolút érték négyzete szolgáltatja.A 3P0 nonett f0(1500)-mezonja esetében minden valószínûség szerint ez lehet a helyzet. Az analízisek azt valószínûsítik, hogy ennél a tömegnél a nonett egy majdnem tiszta s kvark-antikvark mezonjának kell lennie, aminek nagyon gyakran kellene KK-ra bomlania. A gluonlabda egyformán „szereti" mindegyik kvarkot, így a KK módusa annak is viszonylag jelentõs. Az f0(1500)-mezon KK módusa viszont nagyon erõsen el van nyomva, ennek mértéke összhangban van egy gluonlabda -ss--mezon állapotra vonatkozó elméleti számolással.
Kísérleti keresés
Az egzotikus mezonok keresése területén komoly haladást ért el a Genf melletti, tulajdonképpen svájci-francia székhelyû Európai Részecskefizikai Laboratórium (CERN) Crystal Barrel („kristályhordó") kísérlete. A kísérlet során a Low Energy Antiproton Ring (LEAR) speciális gyorsító (inkább „lassító" a helyes kifejezés, mivel a gyors antiprotonokat lassú csomagokba rendezi) a proton 940 MeV/c2 tömegéhez képest sokkal alacsonyabb energiájú antiprotonokat „ráejti" a folyékony vagy gáz céltárgyra. Az antiprotonok a hidrogén atommagjával, a protonnal annihilálódva elõbb két mezonra bomlottak, majd ezek a mezonok tovább bomolva a végállapotban néhány töltött pion és néhány foton volt a végeredmény. A közbülsõ mezonok vizsgálata volt az alapcél, ezek spektrumában jelentek meg azok a részecskék, amikrõl e cikk szól.
A kísérleti berendezés lelke a kísérlet nevét is adó - fotonok (és az itt éppen hiányzó elektronok) detektálására szolgáló - elektromágneses kaloriméter volt. Ez 4p térszögben (98%-os lefedéssel) vette körül a kölcsönhatási pontot és a töltött részecskék detektálására szolgáló drift kamrát. Akaloriméter 1380 darab mesterségesen növesztett CsI(Tl) egykristályból állt, a kristályok összértéke 1 millió svájci frank volt, ez tette ki a kísérlet költségének mintegy 80%-át. A kristályba érkezõ néhány száz MeV energiájú foton meglöki a kristály egyik elektronját, ami kiszakad a kristály kovalens kötésének fogságából, s maga is újabb és újabb elektronokat lök meg, miközben újabb fotonok is keletkeznek. Ígyegy elektromágneses zápor alakul ki az eredetileg egyetlen, nagy energiájú fotonból. A folyamat mindaddig tart, amíg e keletkezõ egyre több és egyre kisebb energiájú foton el nem éri a látható fénytartományát, ami a 300-700 nm hullámhossz határok közé esik. Ez 4 ill. 1,7 eV energiának felel meg, azaz egy 100 MeV-es kemény g-foton több százezer látható fotont kelt. A kísérleti detektor céljainak éppen olyan anyag felel meg, ami átlátszó a látható fény számára. Az így kapott fényjeleket azután fotoelektron-sokszorozókkal tovább lehet majd erõsíteni, rögzíteni. Az együttmûködés mintegy 50 európai és 10 amerikai kutatót fogott össze, aminek része volt a KFKI Részecske- és Magfizikai Kutatóintézetének egy kutatócsoportja is az OTKA hathatós támogatásával.
A kísérlet 1989 és 1996 között mûködött, de az események kiértékelése még ma is tart. 1998-99-re sikerült meggyõzõ bizonyítékot találni a gluonlabdák létezésére az f0(1500)-mezon felfedezésével és tulajdonságainak feltérképezésével. Ugyancsak felfedeztek egy JPC=1-+egzotikus kvantumszámokkal rendelkezõ r(1405)-mezont, ami biztosan nem lehet kvark-antikvark állapot. Tényleges szerkezetének kiderítéséhez további kísérletekre van szükség.
1. Egy antirészecske minden belsõ, töltés jellegû kvantumszáma ellentétes elõjelû, mint az õ részecskéjéé. Ilyen belsõ kvantumszám pl. az elektromos töltés, a szín, a ritkaság, az izospin, a leptonszám, a barionszám, az SU(3)- kvantumszámok stb. A nem belsõ, azaz „külsõ" kvantumszámok pl. az energia, impulzus, impulzusmomentum, spin stb., amik az általunk közvetlenül érzékelt téridõ traszformációkhoz kötõdnek, s nem valamely belsõ szimmetriatulajdonsághoz.
2. Az erõs kölcsönhatás töltésének „szín" elnevezése abból az optikai analógiából származik, hogy ott a három alapszín összekeverése színtelent ad.
3. Ez a= 1,05 10-34 Js redukált Planck-állandó.
4. A hidrogénatom esetén ennek rokona a fõkvantumszám.