TRÓCSÁNYI ZOLTÁN
A proton szerkezete

Írásunk elsõ bekezdéseibõl mindent megtud a kedves olvasó arról, hogy a kutatók mit tártak fel eddig a proton szerkezetérõl. A továbbiakban kicsit közelebbrõl is megismerkedünk a protont felépítõ részecskékkel, a kvarkokkal és a gluonokkal. Célunk nem a proton szerkezetének mennyiségi leírása, hanem az, hogyan lehet egyáltalán ennyit is megtudni egy ilyen piciny objektumról.
Az általunk közvetlenül észlelt világ - amely nem más, mint Naprendszerünk, valamint a világegyetemben észlelt világító anyag, azaz csillagok halmaza - tömegének túlnyomó többségét a proton teszi ki. A proton igen stabil, az elemi részecskék barionok nevû családjának legkönnyebb tagja. Stabilitásáról mindannyian könnyen meggyõzõdhetünk. A felnõtt emberben mintegy 2·1028 darab proton van. Mármost, ha a protonok élettartama, mondjuk, a világegyetem életkorával, 13 milliárd évvel összemérhetõ lenne, akkor egy felnõttben másodpercenként mintegy 1010proton bomlana el, de egyikõnket sem találjuk radioaktívnak. Pontosabb mérések szerint, ha sok protonból találomra kettõt kiválasztunk, akkor legalább 1031évig (ez a világegyetem életkorának 1021-szerese) egyik sem bomlik el.
A proton tehát a világegyetem születése óta mindenütt jelen van. E központi szerepének megfelelõen világszerte sok fizikus tanulmányozza szerkezetét. Azt ugyan már tudjuk, hogy van szerkezete, de mintegy harminc év kutatásai után sem tudunk olyan határozott képet festeni a protonról, mint például az atomról. Tudjuk, hogy a proton igen piciny, jellemzõ mérete 10-15m, ami alatt azt értjük, hogy egységnyi pozitív töltése ekkora tartományban oszlik szét1. Tudjuk továbbá, hogy a proton fõ jellemzõit a benne található három, furcsa tulajdonságú, de legalábbis egyelõre szerkezet nélkülinek tartott (tehát igazán elemi) részecskék, a vegyértékkvarkok határozzák meg. A vegyértékkvarkokon kívül vannak még a protonban gluonok, valamint további kvarkok a kvarktengerben. Utóbbiak a proton bizonyos tulajdonságainak kialakításában fontosak, másokban viszont elhanyagolható szerephez jutnak.
Hogyan próbáljuk felderíteni a mikrovilágot?
Az embert mindig is foglalkoztatta az õt körülvevõ világ felépítése. Kezdetben csak az érzékszerveire támaszkodva próbálta megérteni a világ szerkezetét. Legfontosabb érzékszervünk a szem, a környezetrõl szerzett információ túlnyomó többségét látás útján szerezzük. Szemünk (és a többi érzékszervünk) az életés a fajfenntartás elõsegítésére alakult ki, ezért a környezet apró részleteinek feltárása mindaddig nem volt lehetséges, amíg az újkor hajnalán az ember eszközöket nem kezdett készíteni érzékszervei véges felbontóképességének növelésére. A távcsõvel a nagyméretû, de igen távoli dolgokat figyeljük meg, az egyszerû nagyítóval és a mikroszkóppal pedig a közeli, nagyon piciny méretû tárgyakat. A technológia tökéletesítésével az anyag egyre kisebb léptékû szerkezetét sikerült megismerni, amíg ki nem derült, hogy a mikroszkóp feloldóképessége is véges, bizonyos méretnél kisebb távolságokat nem lehet megkülönböztetni vele.
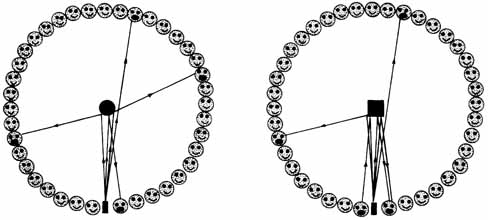
a) b) 1. ábra. A szóráskísérlet makroszkopikus modellje. A körbenállók alkotják az észlelõberendezést. A középre dobott labdák a szórócentrum alakjától függõen másként pattannak vissza. a) Kör keresztmetszetû szórócentrumnál minden irányba hasonló gyakorisággal pattan a labda. b) Négyzet keresztmetszetû szórócentrumnál a labda többnyire visszapattan, vagy elsuhan a centrum mellett, csak ritkán találja el valamelyik élt, akkor, ha a szóródás szöge határozottan nagyobb, mint 0°, de kisebb, mint 180° Könnyû megérteni, hogy bármely nagyító feloldóképességének nemcsak a technológia, hanem a természet törvényei is korlátot szabnak. Amikor egy tárgyat megfigyelünk, a rávetõdõ fény részben elnyelõdik, részben mindenfelé visszaverõdik, és ami ebbõl a szemünkbe jut, abból alakítja ki agyunk a képet. Ilyen megfigyelést nemcsak fénnyel lehet végezni, hanem más (igaz körülményesebb) módon is. Ha sötét szobában egy tárgy alakját szeretnénk felderíteni, megtehetjük, hogy sokan körbeálljuk a tárgyat, majd egyikünk labdákat kezd a tárgyra dobálni, és mindig felkiált az, akihez visszapattan a labda. Egyszerû szerkezetû tárgyaknál néhány dobás elegendõ ahhoz, hogy tudjuk, mi van a kör közepén. Képzeljünk el egy kör alakú hasábot a kör közepére (1.a ábra). Ekkor a labda méretétõl nagyjából függetlenül mindig ugyanaz a szóródási képalakul ki: a hasábot éppen telibe találó labdák 180°-os szögben pattannak vissza; a kicsit félrecsúszók a csúszás nagyságával arányosan egyre kisebb szögben; azok pedig, amelyek annyira félrecsúsznak, hogy elrepülnek a hasáb mellett, azokat a kibocsátás helyével átellenben kapják el. Könnyen elképzelhetõ, hogy ilyen egyszerû szórócentrumnál a szóródási képbõl gyorsan rájövünk a tárgy alakjára. Ha a vizsgálandó tárgynak szerkezete van, akkor a kialakuló szóródási kép a bombázó labdák méretétõl is függ.
Szóródási (vagy a fizikusok nyelvén szórási) kísérletünkben a legegyszerûbb továbblépés az, ha egy négyzetes alapú hasábot helyezünk középre (1.b ábra). Ekkor a labdák egy része, amelyek telibe találják a hasábot, nagyjából 180°-ban visszaverõdnek. A labdák másik része elhúz a hasáb mellett, és a kibocsátás helyével átellenben landolnak. Ha a labda éppen a hasáb élét találja el, meglehetõsen rendezetlen irányba pattan el. Minél kisebb a labda, annál kevesebb az esély arra, hogy eltalálja a hasáb élét. A négyzetes hasáb alakjának egyetlen szerkezete az éle, amelyet úgy tudunk kimérni, hogy egyre kisebb méretû bombázó részecskéket választunk, amivel nõ kísérletünk feloldóképessége. Gondolatkísérletünk fontos tanulsága, ha ismerjük a szórást meghatározó, a labda és a szórócentrum között fellépõ kölcsönhatást leíró fizikai törvényeket, valamint a szóródási képet, akkor elegendõ fejtörés után le tudjuk írni a szórócentrum szerkezetét.
A természetben létezik olyan bombázó részecske, amelynek igen kicsi a mérete az életünket jelentõsen befolyásoló földi objektumokhoz képest. Ez a látható fény. Igaz, a fényre elsõsorban elektromágneses hullámként gondolunk, nem mint részecskére. Ha azonban felidézzük gondolatainkban a Balaton-parti vízhullámokat, gyorsan rájövünk, hogy a hullámoknál a hullámhossz játssza a bombázó részecske méretének szerepét. A vékony nádszálon minden változás nélkül átmennek a hullámok, a csónakról azonban már visszaverõdnek. A látható fény hullámhossza 400-800 nanométerig terjed, tehát az optikai eszközök elméleti feloldóképességének határa a mm-nek ezredrésze, 1 µm, amelyet a legjobb optikájú mikroszkópok el is érnek. A látható fénynél a szórt fénysugarakból agyunk a másodperc töredéke alatt „ki tudja számítani a szórócentrum szerkezetét", azaz a látott tárgy alakját. Csodálatos, milyen sok fizikát tudunk mindannyian anélkül, hogy ez tudatosulna bennünk!Ahhoz, hogy kisebb részleteket is fel tudjunk fedezni egy tárgyon, rövidebb hullámhosszúságú fénnyel kellene néznünk (ultraibolya, röntgen), amelyet azonban szabad szemmel nem látunk, sõt nem is szabad szemünket ilyen sugárzásnak kitenni, mert akkor az élõ szövet roncsolódik. A miniatûr dolgok megismerésében döntõ fordulatot az elektron és a természetes radioaktivitás mintegy száz évvel ezelõtti felfedezése hozott.
Rutherford híres kísérlete
A radioaktivitást a francia Becquerelfedezte fel véletlenül 1896- ban. Azt tapasztalta, hogy az uránsó sugároz, amely elsötétíti a fényképlemezt. Két évvel késõbb az angol Rutherford bebizonyította, hogy a természetes radioaktivitásnak három különbözõ formája van aszerint, milyen messzire tudnak a sugarak a köddel telített kamrában eljutni. A három sugárzásta-, b- és g-sugaraknak nevezte el a növekvõ behatolási távolság szerint. 1902-re Rutherford megmutatta, hogy az a-sugarak anyagi részecskékbõl állnak, amelyeknek pozitív töltésük van, mert erõs elektromos, illetve mágneses térrel eltéríthetõk haladási irányuktól (ehhez az akkoriban elõállítható legerõsebb terekre volt szükség). Az atomok tehát más típusú atommá alakulhatnak át természetes módon úgy, hogy közben anyaguk piciny töredékét kilökik magukból. A középkor alkímiájának célkitûzése bizonyos értelemben megvalósult!
Rutherford felfedezése (amelyért 1908-ban kémiai Nobeldíjat kapott) utat nyitott az atom szerkezetének feltérképezéséhez. Ha az atomból piciny részecskék jöhetnek ki, akkor az anyag akkoriban legkisebb építõkövének tartott atom nem lehet „a-tom", azaz oszthatatlan. Miután addigra az is kiderült, hogy b-sugárzáskor az anyagot az angol Thomson által 1897- ben felfedezett negatív elektromos töltésû részecske, az elektron hagyja el (Nobel-díj: 1906), kézenfekvõ volt feltételezni, hogy az atom valamiféle pozitív töltésû anyagból, és negatív elektronokból áll. A kérdés az volt, hogyan oszlanak el ezek az atomon belül?
Szóráskísérletünkre visszaemlékezve nyilvánvaló, ahhoz, hogy az atom szerkezetét felderítsük, nála kisebb méretû objektummal kell bombázni, és a kialakuló szóródási képet kell analizálni. Rutherfordnak rendelkezésére állt az atomnál kisebb objektum, az a-sugárzásban az atomok egy része lökõdött ki. Száz évvel ezelõtt persze mindez nem volt ilyen egyértelmû még az olyan zseniális tudósok számára sem, mint Rutherford. Akkoriban még nem tudták azt sem, hogy piciny objektumoknál nem igazán beszélhetünk a dolgok hétköznapi értelemben vett méretérõl, mert a világon mindennek kettõs természete van; a tárgyak egyrészt részecske-, másrészt hullámtulajdonságokkal rendelkeznek. Minél kisebb egy tárgy, hullámtermészete annál jelentõsebb, és az elemi részeknél, a francia de Broglie (Nobel-díj: 1929) nyomán, anyaghullámokról szoktunk beszélni. Amikor az atomoknál kisebb méretû objektummal bombázunk valamit, a feloldóképességet a hozzá rendelhetõ anyaghullám hullámhossza határozza meg csakúgy, mint a fénynél.
Rutherford ezt a kvantummechanikai összefüggést még nem ismerhette, hiszen azt csak húsz évvel késõbb fedezték fel, éppen az õ kísérleti eredményeire támaszkodva. Rutherford azonban kiváló kísérletezõi vénával megáldott, kíváncsi ember volt, ami sokszor helyettesíti a tudást.2 Rutherfordot az izgatta, hogy amikor az általa felfedezett a-sugárzást vékony csillámlemezen engedte keresztül (ez is egy szóráskísérlet), akkor az a túloldalra helyezett fényképlemezen elmosódott képet alkotott. A csillám eltérítette az a-részecskéket, amint azok keresztülhaladtak a lemezen. Ez azért volt Rutherford számára meglepõ, mert amikor az a-részecskék elektromos töltésének kimutatására elektromos és mágneses mezõn eresztette át õket - annak ellenére, hogy nagyon erõs mezõket használt - az eltérülés mértéke sokkal kisebb volt, mint amikor pár mm vastagságú csillámlemezen engedte keresztül õket. Felfedezése azt sugallta, hogy a csillámlemez atomjain belül valamiféle, addig elképzelhetetlenül erõs kölcsönhatás hat a részecskék között.
A csillámrejtély tanulmányozására Rutherford szóráskísérletet állíttatott össze két fiatal kollégájával, a német Geigerrel és Marsdennel. Aranyfóliára a-sugarakat bocsátottak, és az átjutó részecskéket minden irányban megfigyelték egy cink-szulfiddal bevont lemezen, amely apró fényfelvillanásokat produkált a becsapódó a-részecskék hatására. A meglepetés akkor érte õket, amikor a szcintilláló lemezt az a-forrás felõli oldalra helyezték: nagy ritkán ott is észleltek felvillanásokat, ami az a-részecskék nagyszögû, közel 180°-os szóródását jelezte.
Miért volt a nagyszögû szórás meglepõ? Rutherfordék tudták, hogy a bombázó részecskék az atom anyagának csak töredékei. Az atomról alkotott addigi modell szerint az atomot pozitív töltésû anyag töltötte ki, amelyben apró negatív töltésû elektronok voltak, éppen annyi, hogy az atom kifelé semleges legyen. Gondoljuk el ebben a képben a Rutherford-féle szórás egy makroszkopikus modelljét! Egy m3 levegõ tömege 1,3 kg. Ehhez képest egy kicsiny acélgolyó elenyészõ tömegû (kb. 10 g). Ha egy acélgolyót elhajítunk a szobában, akkor - a Föld gravitációs vonzásának hatásától eltekintve - egyenesen repül át, és a falba csapódik (2.a ábra). Ha azonban a szobában a m3-enkénti levegõt piciny térfogatra összesûrítjük, mondjuk acélgolyó méretûre, máshol pedig légüres teret hagyunk, akkor dobásaink nagy része továbbra is egyenesen átrepül a szobán, viszont néhány dobással éppen telibe fogunk találni egy sûrített levegõbõl álló kis csomagot, amelynek tömege több, mint százszorosa az eldobott acélgolyó tömegének, így arról a golyó akár 180°-os szögben is visszapattanhat (2.b ábra). Modellünk és a valódi Rutherford-szórás között az a lényeges különbség, hogy az elõbbinél csak a „levegõgolyó" és az acélgolyó tényleges érintkezésekor észlelünk hátraszórást, míg az utóbbi esetben a kölcsönhatás elektromos jellegû, amely valódi érintkezés nélkül is érezteti hatását (távolható). A fizika megfelelõ törvényeinek alkalmazásával azonban ilyen esetben is könnyen meghatározható, hogy a kialakult szórási képhez a szórócentrumnak milyen szerkezetûnek kell lennie. Rutherfordot számításainak eredménye annyira megdöbbentette, hogy jegyzetfüzetében kézírásának jellege is megváltozott. Azt kapta, hogy hátraszóráskor a bombázó a-részecskének az atom közepére sûrített pozitív töltést 10-12 cm-re kell megközelítenie - ez az atom sugarának tízezred része! Rutherford szóráskísérlete szerint a modern atommodell: a 10-8 cm átmérõjû atom közepén egy kb. 10-12 cm átmérõjû térrészen van a sûrített atom tömegének 99,9 százaléka, az atom térfogatának többi része pedig légüres tér, amit néhány pontszerûnek tartott (legalábbis az atommagnál legalább ezerszer kisebb) elektron tölt ki. Ez azt jelenti, hogy testünk és a környezõ tárgyak 99,999 százaléka légüres tér! Megrázó felfedezés, amely alapvetõen megváltoztatta a világról alkotott képünket. Történetünk szempontjából azonban kevésbé a kísérlet eredménye, mint inkább annak módszere a fontos. Ha valamely eleminek tartott részecske szerkezetét keressük, akkor a nagy energiájú részecskékkel való bombázás során a nagyszögû szórás nyújthat felvilágosítást.

a) b) 2. ábra. a) A nagy sebességgel elhajított acélgolyó közel egyenes vonalú pályán halad át a szobában és csapódik a falba. b)Haaköbméterenkénti levegõt olyan kicsire sûrítjük, mint az acélgolyó, a golyó továbbra is egyenes vonalú pályán halad, kivéve, amikor eltalál egy „levegõgolyót", amelyrõl visszapattan
Az elemi részek „periódusos rendszere"
Rutherford és társai felfedezései után jó hetven éven keresztül a mikrovilág fizikájának felfedezése bámulatos gyorsasággal haladt. A szórási kísérletekben a bombázó részecskék energiájának növelésével, valamint a szóródás után kialakuló kép észlelési módszereinek fejlesztésével sok, az atomnál kisebb „elemi részecskét" fedeztek fel a kutatók. Kiderült, hogy az atomok magja sem atom, hanem tovább bontható pozitív töltésû részecskékre, amelyeket Rutherford nyomán protonnaknevezünk, valamint a protonok semleges társaira, a neutronokra, amelyeket Rutherford tanítványa, az angol Chadwickmutatott ki elsõként 1932-ben (Nobel-díj: 1935). Az atommag alkotórészeit összefoglaló néven nukleonoknak hívjuk. Az a-részecske nem más, mint a legstabilabb atommag, a hélium négy nukleonból - két protonból és két neutronból - álló magja.
A neutron felfedezésével majdnem egy idõben találta meg az amerikai Anderson az elsõ olyan elemi részecskét (Nobel-díj: 1936), amely nem az atomon belülrõl jött, hanem a Földön kívülrõl érkezõ kozmikus sugárzásból. A ködkamra felvételei szerint az észlelt részecske ionizáló hatása nagyon hasonlított az elektron ionizáló hatásához. Erõs mágneses térben azonban, ami a mozgó töltéseket kör alakú pályára kényszeríti, az észlelt részecske éppen ellenkezõ irányba csavarodott, mint az elektron, ami az jelezte, hogy elektromos töltése éppen az elektron töltésének ellentettje (-1-szerese) volt. Ez volt az angol Dirac által pár évvel korábban elméleti úton megjósolt antirészecske (Nobel- díj: 1933), az antielektron vagy mai nevén pozitron.Felfedezésével megalapozódott az antianyag létezése, az hogy minden részecskének létezik antirészecskéje. (A modern fizika nyitott kérdése: mi lehet annak az oka, hogy a megfigyelt világ anyagból áll, antianyag ehhez képest csak elenyészõ mértékben található a kozmikus sugárzásban?)
Az 1950-es és 1960-as években több száz, a protonhoz hasonlóan nehéz (az elektron sokkal könnyebb: tömege mintegy kétezred része a proton tömegének) részecskét fedeztek fel, amelyeket többnyire a görög ábécé valamely betûjére kereszteltek: å, L,p, h, r, D stb., és összefoglaló néven hadronoknakhívnak. Mihelyt valamibõl ilyen sok van, az elméleti kutatókat nem igazán az érdekli, van-e még több, hanem az, hogy tulajdonságaik alapján lehet-e rendszert találni közöttük, ahhoz hasonlóan, ahogyan Mengyelejev periódusos rendszerbe foglalta az elemeket. A rendszer mögött mindig az anyag valamilyen alapvetõbb szintjének alkotórészeire jellemzõ, egyszerû tulajdonságok húzódnak.

3. ábra. A barionok Gell-Mann által javasolt két családja. A függõleges menti tulajdonság a ritkaság, az átlós az elektromos töltés. a) Barion oktett: nem ritka tagjai a semleges neutron és egyszeresen pozitív párja, a proton; egyszeresen ritka a három SS-részecske; kétszeresen ritka a két XX-részecske. Az oktett közepén található L-részecskében ugyanazok a kvarkok vannak, mint a szintén semleges S°-részecskében, csak némileg másként elrendezve. b) Barion dekuplett, amelynél degeneráció nincs, és amelynek van háromszorosan ritka tagja, a negatív töltésû WAz elemi részek rendszerezésére az amerikai Gell-Mann és az izraeli Ne'eman1961-ben egymástól függetlenül dolgozott ki rendszert, amely szerint a részecskéket családokba osztályozzuk tulajdonságaik - elektromos töltés, spin, és egy új tulajdonság, a ritkaság (lásd Horváth Dezsõ cikkét) - alapján (3. ábra). Táblázatuk összes tagja azonban nem volt még ismert akkor. 1962-ben az Európai Magfizikai Kutatóközpontban, a CERNben volt egy nemzetközi konferencia, amelyen mindketten részt vettek - Gell-Mann akkor már híres elméleti fizikus volt. A konferencián két új részecske, a negatív töltésû X*- és a semleges X*0 felfedezését jelentették be. Mind Gell-Mann, mind Ne'eman azonnal látta, hogy az új részecskék tulajdonságaik alapján a táblázatukba illenek, és hozzászólásra jelentkeztek. A szót a híresebb Gell-Mann kapta meg, aki a táblához ment, és megjósolta egy további részecske, az addig kísérletileg nem észlelt - nem véletlenül, hiszen háromszorosan ritka - W- létezését. A táblázat többi tagja tulajdonságai ismeretében még a tömegét is megjósolta, miszerint az a proton tömegének 1,8-szerese kell legyen.
„Könnyû" a kísérleti fizikusok dolga, ha ilyen pontosan megmondják nekik, mit kell keresni. 1964-ben az amerikai Brookhavenben meg is találták a Gell-Mann által elõre megadott tulajdonságú részecskét, amelynek a tömege a jósolt értéknél kevesebb, mint fél százalékkal tért el. A sikeres felfedezés azonnal hihetõbbé tette Gell-Mann elméletét, bár a teljes elfogadásig még éveket (a kedves olvasónak azonban csak néhány percet) kellett várni.Milyen modellre is alapozta Gell-Mann a hadronok rendszerét? Alapfeltevése az volt, hogy a hadronok nem elemi részek, alkotóelemeik vannak: a mezonok kettõ (amelyek általában könnyebbek), a barionok pedig három alkotórészbõl állnak. Gell-Mann ezeknek a kvarknevet adta. A kvarkokat nem volt könnyû elfogadni, mert merõben új tulajdonságokat jósolt nekik Gell-Mann. Elektromos töltésük kétféle lehet, az elektron töltésének (+1/3)-a, illetve (-2/3)-a. Soha azelõtt senki nem észlelt az elektron töltésénél kisebb töltésû objektumot - ezért is nevezik azt elemi töltésnek! A kvarkoknak további speciális tulajdonsága is van, amelyet íznekneveztek el, noha nem a hétköznapi értelemben vett ízrõl van szó. Az 1960-as években háromféle kvarkot lehetett íz szerint megkülönböztetni. Késõbb kiderült, hogy a kvarkok hatféle ízben léteznek, a hatodikat csak az 1990-es évek közepén tudták kimutatni. Van a kvarkoknak egy másik tulajdonsága is, amelyrõl Gell-Mann-nak semmiféle kísérleti tapasztalata nem lehetett, és amelyet csupán a kvantummechanika törvényeire alapozva vezetett be Greenberg 1964-ben. Az utóbbi szerint minden kvarkízhez háromféle kvarktípus tartozik. Miután a fizikában a színkeverésben szerepel a hármas szám (a három alapszín a piros, a kék és a zöld, amelyekbõl szemünk az összes színt kikeveri), ezért ezt a tulajdonságot a kvarkok színének nevezték el. Színrõl persze igazi értelemben csak akkor beszélhetünk, ha látható fénnyel megvilágítható az adott tárgy, ami ugyebár a kvark esetében nem lehetséges, hiszen mérete jóval a látható fény felbontóképessége alatt van. Ezek szerint a kvarkból 6·3 =18-féle (és ugyancsak 18-féle antikvark) létezik.A kvark elnevezést Gell-Mann alkotta meg. A szó J. Joyce „Finnegans Wake" címû regényében egy álomban szerepel, nem egészen világos jelentéssel („Három kvark sört Muster Marknak!"), és Gell-Mann-nak egyszerûen csak tetszett a szó hangzása.
A legerõsebb elektronmikroszkóp: a proton nem pontszerû!
A kvarkmodell szerint a kvarkok vagy csoportosan, vagy párokban (ekkor mezonokat alkotnak), vagy hármasával jelennek meg (ekkor barionokat alkotnak). A proton például barion: két u és egy dtípusú kvarkból áll. A kvarkmodell jó ideig csak egy elméleti séma volt a nehéz elemi részek (hadronok) tulajdonságainak rendszerezésére, azonban közvetlen kísérleti kimutatásuk nem történt meg.
Hogyan fognánk a kvarkok protonon belüli kimutatásához, ha meggyõzõ érvek szólnának létezésük mellett? Gondolom, a válasz már minden kedves olvasó számára nyilvánvaló. A protonnál kisebb részecskét kell olyan nagy sebességre gyorsítani, hogy a hozzá tartozó anyaghullám hullámhossza kisebb legyen a proton méreténél, 10-15m-nél. A legésszerûbb megoldás a pontszerûnek ismert, könnyen elõállítható, stabil, elektromosan töltött, tehát elektromos térben gyorsítható részecske, az elektron közel fénysebességûre gyorsítása, és velük a protonok bombázása. Az elektron azért is jó, mert tömege a proton tömegének kétezred része, ha tehát eltalálja a protont, egyszerûen visszalökõdik róla anélkül, hogy a proton lényeges hátralökõdést szenvedne, valahogy úgy, ahogyan a Rutherford szórásban a bombázó a-részecske visszalökõdött a lényegesen nehezebb aranyatommagról.
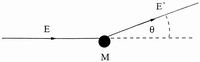
4. ábra. Az elektron-proton szórás leírásához használt fizikai mennyiségek: az elektron szóródási szöge (Q); az elektron végsõ (E') és kezdeti (E) energiája; a proton tömege (M)Mielõtt kísérletünk megvalósításához fognánk, nem árt elgondolkodnunk azon, milyen szórási képet várunk. Jól figyeljünk, mert nehéz rész következik! A szórási kép leírásában a következõ mennyiségek játszanak lényeges szerepet (4. ábra): (i) az elektron szóródási szöge, q (mennyivel tér el eredeti mozgásának irányától); (ii) az elektron energiájának változása (-DE, a negatív elõjel csak megegyezés kérdése): a végsõ (E') és a kezdeti (E) energia különbsége, -DE=E'-E; (iii) a céltárgy tömege (M) (az elektron tömegét egyszerûen nullának vesszük). Minél nagyobb az energia és a szóródási szög, annál nagyobb hatású az ütközés. Az ütközés hatásosságára a Q2-nek nevezett (Q2=4 E E' sin2 (Q/2)) mennyiséget használjuk: kis Q2 lágy ütközést, gyenge feloldóképességet, nagy Q2 viharos ütközést, nagy feloldóképességet jelent. Ezekbõl a mennyiségekbõl képezhetünk egy mértékegység nélküli számot: x=Q2/(2 DE M c2) (c a fénysebesség).

5. ábra. Elektronnak aa-részecskén szóródása során a skálázás, skálázás-sértés, majd újra skálázás észlelése, ahogy az egymáson belüli rétegek növekvõ Q2-tel „láthatóvá" válnak. a-b) Az elektron rugalmasan visszalökõdik a magról, mint egészrõl; a rugalmas csúcs skálázik. c) A rugalmas csúcs skálázásának megszûnése, a mag alkotórészein, a nukleonokon szóródás kvázi-rugalmas csúcsának megjelenése. d-e) Az elektron rugalmasan visszalökõdik a nukleonokról; a kvázi-rugalmas csúcs skálázik. f) A kvázi-rugalmas csúcs skálázásának megszûnése, a nukleonok alkotórószein, a partonokon szóródás csúcsának megjelenése. g-h) Az elektron rugalmasan visszalökõdik a partonokról; a csúcs skálázik. i) Az elektron feloldja a nukleonok további alkotórészeit, a gluonokat és kvark-antikvark párokat. Tovább növelve Q2-et egészen a ma elérhetõ legnagyobb értékekig (~20 000 GeV2), az utolsó ábra skálázását találjuk. Az ábrák rendkívül vázlatosak, sok részlet hiányzik róluk; az átmenetek a valóságban nem figyelhetõk meg ilyen élesen
Pontszerû szórócentrumon szóródva a szóródási kép csak x-tõl függ, mégpedig úgy, hogy x=1-nél megjelenik egy éles csúcs, amelyet a rugalmas szórás csúcsának nevezünk. A csúcs helye, alakja Q2-tõl nem függ - ezt a jelenséget skálázásnak nevezzük. A skálázás azt jelenti, hogy (egy bizonyos tartományon belül) a szórási kép független Q2-tõl (5. a-b ábra). (A bonsai és az óriástölgy alakja nagyon hasonló annak ellenére, hogy méreteik lényegesen különböznek. Ez is skálázás, a fa alakjának skálázása - csak nem Q2-ben, hanem térbeli kiterjedésben.)Ha a céltárgynak szerkezete is van, akkor a szóródási kép Q2-tõl is függ (kis Q2 nem tudja a szerkezetet feloldani, nagy Q2 igen). Belátható, hogy a szórási kép leírható olyan képlettel, amelyben a pontszerû szórócentrumon való rugalmas szóródás formuláját megszorozzuk a szórócentrum szerkezetére jellemzõ úgynevezett alaktényezõvel, amely pedig csak Q2 függvénye: F2(x, Q2) µ f(x)·g(Q2).Tekintsük példaként az elektronnak atommagon való szóródását! Ha Q2 kicsi, akkor az alaktényezõ egységnyi g(Q2)~1, és a szóródási kép a rugalmas csúcs lesz, amely skálázik (5.a-b ábra). Ha Q2 nagy, akkor az elektron képes az atommag szerkezetét feloldani, az alaktényezõ elnyomja a rugalmas szórást, és a rugalmas csúcs skálázása megszûnik. Az elektron most már nem az atommagon, mint oszthatatlan részecskén szóródik, hanem annak alkotórészein, a protonokon és neutronokon. A rugalmas csúcs helyett megjelenik egy kvázi-rugalmas csúcs, amelynek helyét megint csak x=1 adja, csakhogy ezúttal xm=Q2/(2 DE mnc2)=1, ahol mn a nukleon tömege. Ha mondjuk N darab azonos tömegû nukleonból áll az atommag, akkor mn=M/N, és a kvázi-rugalmas csúcs helye x=xm/N=1/N. A kvázi-rugalmas csúcs nem olyan éles, mint a rugalmas csúcs, mert az atommagon belül a nukleonok mozognak, és az elektron hol vele egy irányba, hol ellentétes irányba mozgó nukleonon szóródik, amelytõl az egész kép kicsit elmosódottá válik (5.d ábra). Tovább növelve az energiát, a kvázi-rugalmas csúcs skálázását találjuk (5.e ábra) mindaddig, amíg további réteget nem fedezünk fel, ezúttal a nukleonok alkotórészeit (5.f ábra).
A skálázás, a skálázás-sértés, majd az újra skálázás fenti váltakozása valóban megfigyelhetõ, amikor az elektronok egyre növekvõ Q2 értékekkel szóródnak anyagon, ami az anyag egymásra épülõ rétegeinek (atom, atommag, proton, kvark) létezését bizonyítja. Ezt szemlélteti sematikusan a 6. ábra.

6. ábra. Az anyag egymáson belüli rétegei növekvõ Q2-tel történõ kimutatásának sematikus ábrája
A proton alkotórészeinek kimutatásához az elektronokat elõször a stanfordi kutatóközpontban levõ SLAC-gyorsítóban tudták megfelelõ sebességre gyorsítani 1969-ben. Az elektronok protonokon történõ mélyen rugalmatlan szórása során egyértelmûen kimutatták, hogy az x=1-nél található rugalmas csúcs Q2 növelése esetén Q2=0,5 GeV2-nél3 kezd eltûnni, és helyette x=1/3-nál jelenik meg egy kvázi-rugalmas csúcs, amely Q2>1 GeV2 értékekre határozott skálázást mutat (5. f-h ábra; Friedman, Kendall és Taylor, Nobel-díj: 1990). Megfontolásaink alapján az eredményt úgy tudjuk értelmezni, hogy a protonban három (skálázás 1/3-nál) pontszerûnek tekinthetõ alkotórész van, amelyeket a kísérlet kiértékelésében segítõ amerikai elméleti fizikus J.Björkennyomán azóta is partonoknaknevezünk.
Gondolom, a kedves olvasóban kezd összeállni a kép. Van egyrészt Gell-Mann kvarkmodellje, amely szerint a protonban három kvark van, és kísérletileg sikerült kimutatni, hogy a protonban három pontszerûnek „látott" parton van. Kézenfekvõ a kvarkokat a partonokkal azonosítani, hiszen mindkettõbõl éppen három van a protonban. Az ilyen látszólagos egyezés azonban nem kielégítõ a fizikusok számára. A partonok létezése kísérleti tény, a kvarkmodell pedig, mint neve is mutatja, csak modell. A fizikusoknak azonban elméletrevan szükségük, amely leírja a kvarkok kölcsönhatását úgy, ahogy az elektronok kölcsönhatását leírja az elektromágnességtan (Maxwell, 1860) vagy annak pontosabb változata, a kvantum-elektrodinamika (Feynman, Schwingerés Tomonaga, Nobel-díj: 1965).
Csakhamar megszületett a kívánt elmélet, amelyet (a kvarkok „színesek" lévén) kvantum-színdinamikának neveztek el (Gell- Mann és Fritzsch, 1972). A kvantum-elektrodinamika és a kvantum- színdinamika hasonló elméletek egy lényeges különbséggel. Az elektronok között a kölcsönhatást az elektromos töltéssel nem rendelkezõ elektromágneses tér közvetíti. A kvarkok között azonban a kölcsönhatást az ugyancsak színes gluonokközvetítik, amelyek színességük folytán egymással is kölcsönhatnak. Az elmélet szerint a gluonok átalakulhatnak kvark-antikvark párokká. Ha a gluonok valóban léteznek, és a kvarkok közötti kölcsönhatást közvetítik, akkor a protonon belül is ott kell lenniük, sõt nemcsak azoknak, hanem a belõlük keletkezõ kvark-antikvark pároknak is. Az utóbbiak alkotják a kvarktengert. A modern kísérletek mind a gluonok, mind a kvarktenger jelenlétét megerõsítik. A mélyen rugalmatlan elektron-proton szórásban Q2 további növelésével a skálázás sérül, és kicsiny xértékeknél megjelenik a gluonok és a kvarktengerbeli kvark-antikvark párok járuléka, ami azt mutatja, hogy a három kvarkból álló barionok modellje elegendõ fõ tulajdonságaik szerinti rendszerezésükhöz, de ahhoz például már nem, hogy megadják a felgyorsított proton teljes impulzusát (lendületét) - ahhoz a gluonok és a kvarktenger kvark-antikvark párjai is lényegesen hozzájárulnak.
A proton spinje: egy megoldatlan rejtély
Az elemi részek tulajdonságai két csoportra oszthatók. Az elsõbe olyan mennyiségek tartoznak, amelyek csak meghatározott adagokban (szaknyelven: kvantumokban) változhatnak. Erre példa a 3. ábránrendszerezésre használt elektromos töltés, ritkaság. Ahadronok kvantumos fizikai tulajdonságait a kvarkmodellel tudjuk leírni: a mennyiségnek a hadronhoz tartozó értékét a vegyértékkvarkokhoz tartozó megfelelõ értékek összege adja. A protonban például két u-típusú és egy d-típusú vegyértékkvark van, amelyek töltése az elemi töltésnek (+2/3)-a, illetve (-1/3)-a, ezért a proton töltése az elemi töltés 2·(+2/3)+(-1/3)=1-szerese.
A fizikai tulajdonságok másik csoportja folytonosan változhat, amire az impulzust vehetjük példának. A protonok partonmodelljéhez vezetõ mélyen rugalmatlan szóráskísérletekbõl tudjuk, hogy a proton impulzusát minden alkotórésze (vegyértékkvarkok, gluonok, kvark-antikvark párok a kvarktengerben) impulzusának összege adja.
Az elemi részek fontos jellemzõje a részecskék saját impulzusmomentuma (perdülete) vagy rövid nevén spinje is, amely kvantált fizikai mennyiség, minden részecskére jól meghatározható. Számszerûen a Planck-állandó felének, azaz/2~~5,27·10-35 kgm2/s-nak egész számú többszöröse lehet. A proton, valamint a kvarkok spinje
/2, a gluonoké
. Kvantált mennyiségrõl lévén szó, azt várjuk, hogy a proton spinje a vegyértékkvarkok spinjébõl kapható meg, egyébként nehéz elképzelni, hogy a sok járulékból hogyan kaphatunk éppen
/2-t.
A proton-spin eredetének megfejtésére az 1980-as években több kísérletet is terveztek, amelyek azonban igencsak meglepõ eredményeket szolgáltattak. Kiderült, hogy a proton spinjét nem sikerült a vegyértékkvarkok spinjének összeadásával megkapni, sõt ez utóbbiak összege, a kísérleti bizonytalanságot figyelembe véve akár nulla is lehet. Erre, az addigi proton-képnek ellentmondani látszó eredményre, „protonspin-krízis" néven hivatkoznak a részecskefizikusok. A korábbi elképzeléseknek ellentmondani látszó eredményeknek mindig nagyon örülnek a kutatók, mert azok teret nyitnak új kutatási irányok felfedezésére, új elméleti modellek megalkotására. Különösen így van ez a modern részecskefizikában, ahol az elmúlt mintegy negyedszázad során alig születtek megrázó kísérleti eredmények: szinte minden új felfedezés beleillett a részecskefizika Standard Modelljébe (lásd Horváth Dezsõ cikkét), megerõsítvén azt. A spin-krízis megoldásától ugyan nem várjuk, hogy a Standard Modellt alapjaiban megrendítse, de finomítani fogja azt, amit a proton szerkezetérõl tudunk. Az elméleti szakemberek ötletek tucatjaival álltak elõ megoldásként, azonban mindeddig nem sikerült kísérletileg egyértelmûen bizonyítani egyiket sem. A legegyszerûbb javaslatot hétköznapi nyelven is könnyen megfogalmazhatjuk: a gluonok és a tengerkvarkok valamilyen oknál fogva polarizálódnak, és ez utóbbiak „kioltják" a vegyértékkvarkok spinjét, így a gluonok spinjébõl áll össze a proton spinje. Más elképzelés szerint a kvarkok keringenek a protonban, és a keringésbõl származó pályaimpulzus- momentumot is figyelembe kell venni annak érdekében, hogy megkapjuk a proton teljes spinjét. Létezik a spinkrízis feloldására olyan elképzelés is, amely a kvarkmodell helyett másféle modelljét adná a protonnak. A kérdést ma sem sikerült tisztázni, így szerencsére az olvasónak is jut fejtörõ a proton szerkezetét illetõen.
Miért jó ismerni a proton szerkezetét?
Alapkutatás során mindig nehéz megjósolni, tudja-e majd az emberiség az elért eredményeket a hétköznapokban hasznosítani, és ha igen, akkor milyen formában. A modern világ eddigi története azt mutatja, hogy az eredmények zöme csak a tudomány továbbfejlõdése szempontjából érdekes, és néha akad egy-egy, amely alkalmazást nyer a technikában, vagy akár alapjában változtatja meg életünket. Ráadásul azok az eredmények, amelyek olyan lényegesnek bizonyulnak, sokszor nem is a tervezett kutatási irány termékei, hanem az ahhoz kapcsolódó véletlen folyamatoké. Példaként megemlíthetnénk a radioaktivitást vagy a biológiában a penicillin felfedezését, de ide sorolhatjuk a számítógépes világháló létrejöttét is, amely eredetileg a részecskefizikai kutatásokban kialakult kutatócentrumok közötti információáramlást volt hivatott elõsegíteni. Ezen értelemben a proton szerkezetének kutatása máris alapjában változtatta meg életünket. Közvetlenebb értelemben a proton szerkezetének minél pontosabb ismerete pillanatnyilag a részecskefizika továbbfejlõdése szempontjából fontos kérdés.
A modern kísérleti részecskefizikában a gyorsítókat nemcsak az eddig bemutatott mikroszkóp formájában használjuk, hanem úgy is, hogy minél nagyobb energiát sûrítsünk a lehetõ legkisebb térfogatra, és ezzel a világegyetem születésekor fennálló körülményeket hozzunk létre abból a célból, hogy a korábban még meg nem figyelt részecskéket, az anyag új halmazállapotait észleljük. Einsteinhíres E=m·c2 összefüggése szerint az energia (E) és a tömeg (m) egymással arányos mennyiségek, az arányossági tényezõ a fénysebesség (c) négyzete. Ezt az összefüggést használják fel az atomreaktorok úgy, hogy piciny tömegeket nagy mennyiségû energiává alakítanak; és ezt használják a részecskegyorsítókban arra, hogy energiabefektetés árán tömeget hozzanak létre, méghozzá korábban ismeretlen formában. Az ideális gyorsító az, amely egy részecskét és annak antirészecskéjét azonos sebességre gyorsítja fel egymással szemben és úgy ütközteti azokat. Az ütközés során a két részecske megsemmisül, a felszabaduló energia pedig elegendõ lehet ahhoz, hogy új típusú részecskék keletkezzenek. Ilyen ütközõgyûrûs gyorsító a genfi székhelyû CERN kutatóközpont LEP gyorsítója, ahol elektront és pozitront ütköztetnek, és többnyire egészen más részecskék érkeznek az észlelõrendszerbe (Rutherford szcintillálólemezeinek modern megfelelõi). Mintha két követ összeütve kenyerek jönnének elõ.
Az elektron-pozitron ütközõgyûrûben az ütközésben felszabaduló energia, és így az újonnan keletkezhetõ részecske tömege viszonylag szûk tartományra rögzített érték, a két ütközõ részecske teljes energiája. Ez akkor hasznos, ha már tudjuk a kelteni kívánt részecske tömegét (elméleti megfontolásokból, mint Gell-Mann tudta az W- tömegét), azonban ismeretlen részecskéknél ez nincs így. Ilyenkor jobb, ha ugyanazzal a gyorsítóval sokféle energiájú ütközést tudunk létrehozni, és ekkor, szerencsés esetben lesz olyan energiájú is, amely éppen egy új részecske tömegének felel meg: azt akkor felfedezzük. Ha még emlékszünk arra, hogy adott energiára gyorsított protonok halmazában a kvarkok energiája meghatározható valószínûséggel bármilyen értéket felvehet, kézenfekvõen adódik az univerzális gyorsító megalkotásának lehetõsége: protonokat kell protonokkal ütköztetni. Ilyen folyamatok során többnyire a két protonban repülõ kvarkok közül fog egy-egy ütközni.4 Ahhoz, hogy a szórási képbõl pontos mennyiségi következtetést tudjunk levonni, fontos tudni, milyen volt a kezdeti állapot, azaz a két ütközõ kvark az õket hordozó protonok mekkora energiáját szállította. Többek között ezt a kérdést tanulmányozzák nagyon alaposan a Hamburg melletti DESY-ben, ahol 27,5 GeV-re felgyorsított elektronokat vagy pozitronokat ütköztetnek 820 GeV-re felgyorsított protonokkal.
IRODALOM[1]Frank Close, Michael Marten, Christine Sutton: The Particle Explosion, Oxford University Press, New York Tokyo Melbourne, 1987
[2] Simonyi Károly: A fizika kultúrtörténete, Gondolat, Budapest, 1986
[3] Leon Lederman: Az isteni a-tom, avagy mi a kérdés, ha a válasz a Világegyetem, Typotex, Budapest, 1996JEGYZETEK
1.10-15 m olyan piciny, hogy semmiképpen nem tudjuk hétköznapi méretekkel érzékeltetni. Legfeljebb annyit mondhatunk, hogy a proton akkora a gombostûfejhez képest, mint a gombostûfej a Naphoz képest (amelyeknek nagyságát ugyancsak nem tudjuk megfelelõen felfogni, hiszen nincs közvetlen tapasztalatunk róla).
2.Hogy ez mennyire így van, azt a gyermekeken könnyen megfigyelhetjük. Mai példát hozva: a gyermekek egy új számítógépes program használatát sokszor még azon felnõtteknél is hamarabb kiismerik, akik járatosak a számítógépek világában. Ezzel a szerzõ nem a tudás fontosságát kívánja lebecsülni, hanem a kísérletezõ, kíváncsi szellem szerepét hangsúlyozni.
3.1 GeV = egymilliárd elektronvolt, ahol 1 elektronvolt az az energia, amelyre az elektron szert tesz, amikor 1 volt potenciálkülönbséget átszel.
4. Sokkal ritkábban elõfordulhat a kétszeres szórás, azaz amikor két-két kvark ütközik egyszerre, ennek azonban kisebb a valószínûsége ugyanúgy, mint ahogy az sokkal gyakoribb, hogy az úton két autó ütközzön, és az ritkán fordul elõ, hogy ugyanazon a helyen egyidõben két-két autó találkozzon. Persze nagy sebesség és nagy forgalom mellett autópályákon a tömeges karambolok is elõfordulnak - ehhez hasonlóan a CERN-ben tervezett következõ gyorsító, az LHC esetén már gyakoribbak lesznek a kétszeres szórási események.