Végh Petra-Riegler Márton
Jurisich Miklós Gimnázium, Kőszeg
Nem kell ahhoz zseninek lenni, hogy a matematika egy-két érdekességét felfedezzük. Dolgozatunk témájához az adta az ötletet, hogy egy rajzóra alkalmával elkezdtünk játszani a pontokkal és a vonalakkal. Az eredmény több mint érdekes volt, ahogyan az egyenes vonalakból görbéket alakítottunk ki. Mondhatni háromdimenziós képeket kaptunk. Vajon mi ennek a magyarázata?! A választ a matematika adta meg.

Így kezdődött játékunk a vonalakkal, ami idővel már szenvedéllyé vált. Az egyszerűbb ábráktól haladtunk a bonyolultabbak felé. Munkánkat színezéssel még látványosabbá tettük. Végül egy merész ötlettel a tollal húzott vonalat lecseréltük fonalra, eljutva ezzel a fonalgrafikához. Építsük hát fel lépésről lépésre a csodát, bizonyítva ezzel is, hogy az egyszerű dolgok valójában nagyok.
Vonalak a koordinátarendszerben
Induljunk ki Descartes
koordinátarendszeréből. Tekintsük az első síknegyedet. Kössük össze
rendre az x és y tengely pontjait a következő
rendszer szerint: az (1; 0) pontot a (0; yi) ponttal,
a (2; 0) pontot a (0; yi-1) ponttal, a
(3; 0) pontot a (0; yi-2) ponttal stb.,
az (xi-1; 0) pontota a (0; 2) ponttal,
az (xi; 0) pontot a (0; 1) ponttal.
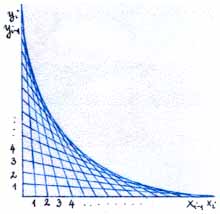 |
| 1. ábra. Az egyenesekből görbe lesz |
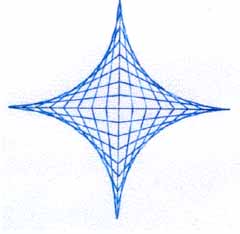 |
| 2. ábra.
Ábránk mintha kilépne a papír síkjából |
 |
| 3. A látvány színezéssel fokozható |
Egyenesekből görbét varázsoltunk a lapunkra (1. ábra). Folytassuk a feladatot, készítsük el a rajzot mind a négy síknegyedben. Ábránk mintha "kilépne" a papírlap síkjából, érzékeljük a teret (2. ábra). Persze, ez csak egy optikai csalódás. Fokozhatjuk a látványt színezéssel (3. ábra).
Kocka és lapátlói
A kockát már gyermekkorunktól jól ismerjük. Tartozéka például a különböző társasjátékoknak vagy a pókernek. Szemmel jól érzékelhető hat egybevágó négyzetlapja. Mi most egy "sarkainál meghajtott csíkos kendőt" varázsolunk bele.
Készítsünk egy tetszés szerinti a oldalélű kockát. Húzzuk meg a két szemközti négyzetlap átlóját (a rajtuk átfektetett egyenesek kitérők legyenek), osszuk fel ezen átlókat egyenlő részekre, és az osztópontokat a 4. ábra szerint kössük össze. A kapott nyeregfelületet a színekkel tehetjük még látványosabbá.

4. ábra.
Így varázsoltunk a kockába sarkainál meghajlított csíkos kendőt
Pontok és vonalak
Gyönyörködjünk tovább a vonalakban oly módon, hogy rajzunkhoz két pontot is segítségül hívunk. Ezeket tetszés szerint válasszuk ki lapunk síkjában. Nevezzük őket A és B pontnak.Szükséges még, hogy lapunk széleit egyenlő részekre osszuk fel. Valamennyi osztópontot kössük össze A és B pontokkal. Az egymást keresztező vonalak különböző sokszögeket határoznak meg. Kiindulva egy sarokból, minden másodikat kiszínezzük. Az eredmény egy térhatású kép lesz (5. ábra). Tapasztaltuk, hogy problémánk akkor adódik a színezésnél, ha a véletlen folytán A, B és valamelyik osztópont egy egyenesre esik.

5. ábra.
Az egymást keresztező vonalak különböző szögeket határoznak meg
Hasonló térhatású képet kaphatunk úgy is, ha egy szabályos sokszögből indulunk ki, és meghúzzuk összes átlóját. Ezek száma n oldalú sokszög esetén: n(n-3)/2. Legyen n páros, mivel ellenkező esetben gondba leszünk a színezéssel. A 6. ábra egy szabályos tizenkétszög.

6. ábra.
Térhatású képet kapunk úgy is, ha egy szabályos sokszögből indulunk
ki
Körök-körvonalak
Tekintsünk egy síkot, és annak egy tetszőleges O pontját. Azon pontok halmaza a síkon, amelyek O-tól egyenlő távolságra vannak, az Oközéppontú körön helyezkednek el. Sugara az adott távolság. Különböző és egyenlő sugarú körökkel káprázatos ábrák készíthetők.
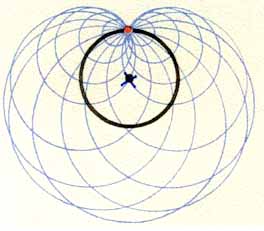
7. ábra.
Különböző sugarú körök, melyek középpontja a fekete körön van,
és a körök mindegyike átmegy az x-szel jelölt ponton
A 7. ábrán különböző sugarú köröket rajzoltunk. Mindegyik kör középpontja a fekete körön van.

8. ábra.
Azonos sugarú körök, melyeknek középpontja egy helyen van
A 8. ábrán azonos sugarú körök láthatók. (Hasonló motívumokkal találkozhatunk a templomok színes ablakainál.)
Vonal helyett fonal
Ilyen ábrákat nemcsak vonalzóval és tollal készíthetünk, hanem fonallal is. Ezt a művészetet fonalgrafikának hívják. A technika elsajátításához persze jól jön némi ügyesség, és jó tudni, hogy tűvel bánni nem éppen veszélytelen dolog.
Aki tehát a ceruzát, a tollat és a vonalzót tűre és fonalra cseréli, tartsa szem előtt az előbbi intelmeket. A grafika alapját a szögek alkotják, melyek lehetnek derékszögek vagy hegyesszögek. Célszerű kartonra dolgozni, mivel a papírlap vékony a varráshoz. A mintát előzőleg el kell készíteni, meg kell tervezni. (Toll és vonalzó tehát továbbra is szükséges.) Ezt ráhelyezzük a kiválasztott kartonra, majd kilyuggatjuk. A tűt a következők szerint vezessük: Induljunk ki az A pontból, ezt kövesse az 1, majd 2, 3… stb. (9. ábra).
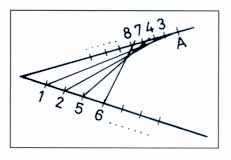
9. ábra.
A fonalgrafika készítésének sorrendje
Körök
esetében osszuk fel a kör kerületét egyenlő részekre. Kiválasztunk
a körvonalon egy pontot (A), tekintsük ezt kiindulópontnak. A
fonalat A-ból a körvonal másik osztópontjához vezetjük (1),
majd az 1-sel szomszédos 2-ből az A-val szomszédos 3-ba,
a 3-sal szomszédos 4-ből a 2-sel szomszédos 5-be, és így tovább (10.
ábra). A kapott napmotívum annál szélesebb, minél nagyobb ez a távolság.
Ha éppen az átmérővel egyezik meg, akkor a fonalak a kör középpontjában
metszik egymást.

10. ábra.
Fonalgrafika
A vonalakkal való játékunk ráébresztett minket arra, hogy a matematikaszép és örömet okoz. Valójában persze olyan dolgokat fedeztünk fel, amelyeket a tudomány nagyjai előttünk sok-sok évvel ezelőtt már megtettek. Mégis átéreztük a felfedezés örömét.
Ismertek előttünk például az 1908-ban Pécsen született, később Párizsban letelepedő Victor Vasarely grafikái. Őt is kezdettől foglalkoztatták a síkábrázolás térproblémái. Tanulmányai igazolják, hogy vizsgálta az egymásra vetített párhuzamos vonalak permutációját és az így elért perspektivikus hatásokat. Vasarely Arlequin (1935) sorozata már teljességében magában hordja a térilluzionizmust, a kinetikus perspektíva gyökerét. Pécsen, szülőházában berendezett múzeumát számtalan alkotásával - amelyeket maga a művész ajándékozott a városnak - nekünk is volt alkalmunk megtekinteni.

"Fonalas
kocka" lapjai
Vasarely foglalkozott a grafikai mozgás, valamint a színek kölcsönhatásából eredő vibráció kérdésével is. Ezzel kapcsolatosan a hatvanas évektől egy új kifejezés is életre kelt. Ez az op-art (=optical art) művészete.
Nem vagyunk művészek, csupán diákok, akiket rabul ejtett a rácsodálkozás öröme. Goethe szavaival élve hisszük és valljuk, hogy "a zsenialitás fele szorgalom".
Az írás szerzői
Diákpályázatunkon a Martin Gardner matematikaprofesszor által kiírt
Matematika különdíj kategóriában I. díjat kaptak.
| Természet Világa, | 134. évfolyam,
12. szám, 2003. december http://www.chemonet.hu/TermVil/ http://www.kfki.hu/chemonet/TermVil/ |