| Károlyházy
Frigyes Ördöngös téridő |
 |
Prológus
Kénkőszag, füst,
csattanás - megjelenik a tudós szobájában az ördög, és a tudós lelkét
kéri. Fiatalságot, gazdagságot ígér. A tudós csak legyint.
"Fellebbentem ön előtt a titkok fátyolát!" - A tudósnak felcsillan a
szeme.
"Tessék, itt a lelkem, előre odaadom. Csak mondja meg, hogy a sugárzás
atomos szerkezetű-e, vagy hullámjellegű, vagy esetleg más, és miért."
Az ördög boldogan elcsomagolja a lelket. "Én magam nem foglalkozom ilyesmivel,
de van egy csoportunk erre a célra, a Feneketlen Tudás Ördögei. Rövidesen
hozom a választ."
Pár nap múlva újra megjelenik az ördög, és fakó arccal visszaadja a
tudós lelkét.
"Ők sem tudják" - mondja leverten.
Ezt a jelenetet "A tudós lelke" című, pár oldalas humoreszkből kölcsönöztük. Az írás Feleki László "Le az olvasókkal" c. vidám kötetében jelent meg, 1960-ban.
Bár a szerzője alighanem kézzel-lábbal tiltakozna a komolyság vádja ellen, ez a kis kroki nagyon telibe talál valamit. A XX. század elején, tudjuk, forradalom zajlott le a fizikában. A tudás új pilléreivé mindenekelőtt a relativitáselmélet és a kvantumelmélet váltak. A kibontakozó modern fizikáról mindenki szívesen elhinné, hogy összetettebb, "nehezebb", mint a régi volt. Hosszadalmas dolgokat hajlamosak vagyunk elfogadni részletekbe menő magyarázat nélkül is. De az új állítások, éppen a leglényegesebbek, egyáltalán nem bonyolultnak, hanem nagyon is világosan áttekinthető képtelenségnek tűnnek. Az ilyesmivel szemben viszont senki nem maradhat közömbös. Például: elindítunk egy fényjelet, majd egy idő után, amikor már messze jár, utánaeredünk. A fény hozzánk viszonyított sebessége nem változik meg attól, hogy üldözőbe vettük. Lehetett-e más annak idején az utca emberének a reakciója egy ilyen kijelentésre, mint az, hogy "vagy szélhámos, aki ilyet mond, vagy pokolba az egész fizikával!" A kvantummechanika sem maradt le az "egyszerű, csupáncsak lehetetlen" dolgok kínálatában. Megszületése után nem sokkal sort kerített olyan méréssorozatra, amelyben az elektron, az atomfizika akkori főszereplője, azt árulja el magáról, hogy ő egyszerre pontszerű lény és nagy méretű, kiterjedt felhő. Mi ez, ha nem fából vaskarika? A hasonló "fogalmi dugóknak" se szeri, se száma. A helyzet a XX. század eleje óta "csak romlott", az észbontóan szemléletellenes konstrukciók elfogadása, sőt keresése általában jellemzi a modern fizikát.
Kép és gondolat
Mi lehet az oka, hogy éppen a XX. század elején válik ilyen "tréfás kedvűvé" vagy "gonoszkodóvá" a tudomány? Vagy talán nem is helyénvaló a vád, csupán történeti rövidlátás, hogy csak a saját korunk dilemmáit érezzük át igazán? Is-is.
Valóban nevezetes korszakhoz értünk el a XIX. és a XX. század fordulóján.
Röviden: a tudományos gondolkodás végérvényesen "kinőtte" az idegrendszer ösztönös tudását.
Már egy kutya is rendelkezik bizonyos "klasszikus fizikai" ismeretekkel. Idejében félreugrik a feléje hajított kő elől, ezzel jelezve, hogy "tisztában van Newton első axiómájával". Ha valami gőzölög vagy izzik, abba nem lép bele, "tudja", hogy forró. Van némi képe a különböző jelenségekről. Az érzékletes benyomások, szemléletes képek ilyenfajta seregét hívhatjuk ösztönös tudásnak. Szakszerűbben kifejezve, az evolúció során kiépült egy modell a világról a kutya (s ugyanígy a majom, vagy - feltehetően - az előember) idegrendszerében.
A mai emberi gondolkodás csodájának kezdete az eszmélkedés, az ember tudatra ébredése, a spontán magyarázatkeresés, a mítoszok születése. Aztán a görögök felfedezték az érvelő gondolkozás, a tudomány, a logika erejét, és tudatos spekulációval próbálták a különböző széteső benyomásokat egységbe foglalni. Innen kezdve hosszú-hosszú időn át igyekezett az ember az érzékletes tapasztalatok és a szigorú gondolkodás összhangját megteremteni, több-kevesebb sikerrel. Bár örökös kételyek közepette, mégis gyakran tűnhetett úgy, hogy az alapvető tapasztalatok s a belőlük kinőtt képzetek köre elég tág ahhoz, hogy a rájuk épülő spekulációkat hordozza, és hogy megfigyeléseink és elgondolásaink finomodhatnak, változhatnak ugyan, de a közvetlen érzékelés alapelemei mindig kiindulásul szolgálhatnak.
Egy nevezetes példa. Az ősember tudta, hogy ha egy madarat le akar dobni kővel, akkor a célpont felé kell hajítania a követ, s ha egyszer eldobta, akkor a kő "magától megy" a madár felé. Azt is tudta, hogy ha egy nagyobb vadat elejtett, azt vonszolni kell, és mihelyt megállunk, a zsákmány is megáll. A görögök voltak az elsők, akik a két, tulajdonképpen egymásnak ellentmondó benyomást tudatosan próbálták egyeztetni. Azt választották közös alapnak, hogy a mozgás fenntartásához erő kell. Kispekulálták, hogy a repülő kőre valamiképpen hat a környező levegő, az tolja előre. Az újkori fizika elején az értelmezés mintegy megfordult. Galilei óta azt tartjuk, hogy a kő mozgása természetes, a vadászzsákmány pedig - ha nem vonszoljuk tovább - nem azért áll meg, mert nem hat rá erő, hanem azért, mert hat rá erő, tudniillik a súrlódás. A világkép ilyen változását bízvást nevezhetjük forradalminak, de a szerepet játszó fogalmak (mozgás, erő, súrlódás) egyáltalán nem merítik ki hétköznapi érzékelésünk kapacitását. (Hasonlóképpen, a Jupiter holdjait mindenki megpillanthatta, aki hajlandó volt távcsőbe nézni. És lehet, hogy Kolumbusz hajósait még hisztérikus állapotba hozta az ismeretlentől való félelem, de felfedezésüket egy márvány földgömb kézzelfoghatóvá teszi.)
Ezt a kapacitást lépte túl a modern fizika.
Természetesen csak Darwin után érthettük meg, hogy az a modell a világról, amelynek alapjait (vagy az alapok gyors kialakításához szükséges képességeket) születéskor magunkkal hozzuk, nem abszolútum (mondjuk a priori kategóriák készlete), hanem evolúciós termék, tehát egyrészt igenis (évmilliós) "tanulásra" támaszkodik, másrészt nem feltétlenül végső szó, nem "maga a tökéletesség". De a "belátás gyorsaságával" nem dicsekedhet a kutatók közössége. Keservesen és lassan vált általánosan elfogadottá, hogy a közvetlen, érzékletes benyomásokra alapuló szemlélet, mint alap, a köznapi tapasztalatokból "foltokban" összeszőtt tudományos gondolatokat még elbírja, de a kifinomult műszerekkel, rafinált megfigyeléssel kapott összefüggéseket már nem képes hordozni. Úgy tűnik, hogy csupán az agyműködés, a megismerési modellek vizsgálatának eredményei teremtettek olyan légkört a XX. század utolsó harmadában, amelyben az egyre újabb és újabb absztrakcióknak és az érzékletes benyomásoknak a viszonya (értelemszerűen az egész élővilágra kiterjesztve) elfogulatlanul boncolhatóvá vált. Iránymutatónak az a - részben már korábbi eredetű - felismerés bizonyult, hogy az érzékelés "adatai" nem egyszerűen nyersanyagot jelentenek a tudás, a gondolkodás számára, hanem már önmagukban bizonyos "elméleteket" és az aktuális ingereket ezekhez illesztő "hipotéziseket" takarnak. Ez általában nagy segítség a (bármilyen szintű) tudati tevékenység tehermentesítésére, de hajlamos eltorlaszolni az utat, amikor valami merőben újat kell befogadni.
A modern fizikai forradalom ismeretelméleti helyretevésének lassúsága azonban nem véletlen. Hadd emlékeztessünk Steven Weinberg megállapítására, aki a "fizika éve" alkalmából a Természet Világában indított sorozat nyitó tanulmányában ezt mondja: "1900-ban a tudósok általában azzal a feltételezéssel éltek, hogy a fizika, a kémia és a biológia mindegyike saját autonóm törvényekkel rendelkezik. … (a fizikusok) fel sem tételezték, hogy a fizika feladatai közé tartozna a kémia vagy az élet magyarázata. A XIX. század másodikfelében élő fizikusok önelégültsége a mértéke annak, hogy mennyire korlátozottak voltak a fizika ambíciói."
A fizika korabeli "igénytelenségéről" egy másik Nobel-díjas fizikus, Wigner Jenő is szót ejt. Önéletrajzi visszaemlékezésében leírja, hogy gyerekkorában az ő iskolai fizikakönyvében még ez állt: "A fizika olyan jelenségekkel foglalkozik, amelyek során a testek nem szenvednek lényeges változást."
Nos, ha egyszer a fizikusoknak eszébe sem jutott, hogy érdemben beleszólhatnának a biológia belügyeibe, akkor arra sem gondolhattak, hogy éppen a biológia nyújthat "életmentő" segítséget a Lorentz-transzformáció vagy a kvantumugrások fogalmi görcseinek a "kikezelésében". Kérdéses, hogy akadt-e fizikus a XIX. és XX. század fordulóján, vagy akár az utána következő néhány évtizedben, akiben Darwin neve vagy az evolúció gondolata az új fizika paradoxonaival kapcsolatban egyáltalán felmerült.
De megkockáztathatjuk azt a megjegyzést, hogy például az élő anyag élettelenből való keletkezésére vonatkozó spekulációk időszerűségét a biológusok túlnyomó többsége sem vette komolyan a XX. század első harmadában. Csak Watson és Crick korszakalkotó (a DNS szerkezetét tisztázó) felfedezése után vált az egész tudományos világ élményévé, hogy a modern fizika a tudomány minden ágában (a DNS esetében az anyag szerkezetének kvantummechanikai megvilágításával) döntő segítséget nyújt, ami - megfordítva - "érzékelhetővé" tette mindenki számára, hogy a relativitáselmélet vagy a kvantummechanika újszerű igazságait komolyan kell venni. (Alighanem éppen ez indította el a kognitív tudományok felvirágzását.)
Van-e valami mentsége az "igénytelenségre" a XIX. századi fizikának?
Egy harmadik Nobel-díjas tudós, François Jacob, a mítosz és a tudomány viszonyát elemezve a következőket mondja: "Ami az egységet és összefüggőséget illeti, a mitikus magyarázat gyakran jobban működik a tudományosnál… A természettudomány kevésbé látszik nagyratörőnek a mítosznál. Sőt, a modern természettudományok kezdeteit éppen arra az időre lehet datálni, amikor az olyasféle általános kérdések helyébe, mint: »Hogyan teremtették a világot? Miből van az anyag?«, szerényebb kérdések léptek, olyanok, mint: »Hogyan esik le egy kő? Hogyan folyik a víz egy csőben? Mi az útja a vérnek a testben?« … A tudományos módszer… a világszemlélet széttöredezéséhez vezetett… A tudományos ismeretek gyakran magányos szigeteknek látszanak."
Igen, a XIX. század még "túl közel van" a XVII.-hez.
A klasszikus fizika nagymértékben leíró jellegű. Vannak hajlékony tárgyak és vannak törékenyek stb. Természetesen a klasszikus fizika is bővelkedik élményt adó következtetésekben. (Izgalmas dolog lehet megérteni - különösen az erre kínálkozó életkorban! - , hogy az elengedett lufi azért száll felfelé, mert a Föld minden testet vonz.) De a tapasztalatra való sűrű támaszkodásért azzal kell fizetni, hogy az összefüggések nem lesznek túlságosan messzemenőek. Arról úgyszólván semmit sem tudunk mondani, hogy ha az ablaküveg nem engedi át a futball-labdát, akkor miért engedi át a fényt.
A modern fizika ezzel szemben mélyen a közvetlenül érzékelhető "felszín" mögé lát, a korábbinál sokkal átfogóbb megértéshez vezet. A modern fizika meg tudja mondani, miért a vas mágnesezhető, nem a réz, miért az üveg átlátszó, nem a fa. Csakhogy ennek is ára van.
Hadd érzékeltessük ezt a fény példájánál maradva. Miért nem akad el a fény az ablaküvegben, vagy miért nem töri össze? Kézenfekvő feleletként csak az kínálkozik, hogy a fény "ártalmatlan" hullámjelenség. (Valóban, a szomszéd lakásból a veszekedés "szépen" áthallatszik a falon.) De akkor mivel magyarázhatjuk, hogy nyár elején, néhány órával az első, meggondolatlan napozás után, bőrünk égni kezd? A felhólyagzott bőr tanúsága szerint a napsugár inkább parányi lándzsások hadserege, mint ártalmatlan hullám.
Melyik hasonlat a helyes? Egyik sem, a fény sem a hullámzó Balatonhoz, sem a rohamozó sereghez nem hasonlít igazán. (Ezért jut hol az egyik, hol a másik, "egymást ütő" hasonlat az eszünkbe. Képzeljük el, hogy valamilyen idelátogató E. T., aki semmilyen földi élőlénynek nem hasonmása, egy röpke pillanatra láthatóvá teszi magát. Az lenne a csoda, ha utána a szemtanúk beszámolói nem mondanának ellent egymásnak.)
A modern fizika világosan meg tudja fogalmazni, hogy mai ismereteink szerint mik a fény (vagy az elektronok) alapvető jellemvonásai. Ehhez azonban elvont, matematikai ízű koncepciókra van szüksége. Például egy olyan magasabb rendű fogalmat kellett kovácsolnia, amelynek a makroszkopikus hullámokra, illetve lövedékekre emlékeztető megnyilvánulás csupán egy-egy vetülete, olyanféleképpen, mint ahogy egy konzervdoboz árnyéka lehet kör vagy négyszög.
Az új fogalmak érthetően elvontak. Erejüket éppen annak köszönhetik, hogy a szétesőt (magasabb rendű) egységbe képesek foglalni. Tartalmuk így gazdagabb annál, amit a nevük, vagy a rövid leírásuk általában sugall. Ugyanis a rövid, népszerűsítő jellemzések, vagy a nevek (valójában még a legelszántabb elméleti fizikus szóhasználatában is!) a lehetőség szerint őrzik azoknak a "provinciális" fogalmaknak a miliőjét, amelyekből az új fogalmak kikerekedtek, hiszen minél megfoghatatlanabb valami, annál szívesebben hivatkozunk rá valamilyen egyszerű, szemléletes jelöléssel.
Ez a körülmény azonban az érdeklődő kívülállók - régebbi kifejezéssel, a "művelt laikusok" vagy a "nagyközönség" - szempontjából permanens kudarcélmény forrása. A "képtelenség" lehangoló érzése akkor vesz rajtunk erőt, amikor a gazdagságot a megszokott, szegényes keretbe próbáljuk beleerőszakolni. (Ezt viszont akarva-akaratlan elkövetjük.) Márpedig ma úgyszólván mindenki érdekelt kívülálló - a modern fizika eredményei úgy vesznek körül bennünket, hogy nem tudomást venni róluk nem lehet. A társadalom számára nem közömbös, hogy - reakcióképpen, különböző áttételeken keresztül - eluralkodik-e egy olyan "ellenséges hangulat," miszerint "az életben a fizikára nincs szükség".
Nagyon elkelne legalább egyetlen olyan nyomon követhető "metamorfózis", amelyben egy "naiv" képzet valamilyen teljesítőképesebb, átfogóbb, cserében nem szemléletes fogalommá alakul át. Ebbe a fába fogjuk a fejszénket vágni. De előbb még a letűnt időknek kell teljes igazságot szolgáltatnunk.
Az emberi megismerés fejlődésének a csodája, hogy a szellem mindig előbbre járt a kézzelfoghatónál. Előbb gyönyörű mítoszok teremtésével zárta le, tette teljessé a világképet. Azután pedig, mihelyt a görögök ráéreztek a kritikus gondolkodás ízére, csakhamar odáig jutottak (2500 évvel ezelőtt!), hogy képesek voltak átélni a szemlélet és a tudatos spekuláció konfliktusát.
Az iskolai emlékeinkből jól ismert aporiák közül egyet megemlítünk, mivel felhasználjuk a későbbiekben. A mozgás mibenléte talányosnak tűnt, éspedig az alábbi okból.
1. ábra. Egydimenziós tér
Az ókori világkép, az iskolában megszokott leegyszerűsítéssel élve, sztatikus. Az arisztotelészi fizikában a testek természetes állapota a nyugalom a megfelelő helyen. Számunkra most nem az a nyilvánvaló (mindennapos, de mégis tudatosan is megfigyelt) tapasztalat a fontos, hogy "a tűz" felfelé száll, a kő leesik, hanem az az öntudatlan folyamat, amelynek során a "puszta hely" képzete kialakul és szemléletünk "hallgatólagos" részévé válik. A nyugalom szó egy helyen maradást jelent a számunkra, a mozgás helyváltoztatás. A mozgó tárgy nem egyik testtől a másikig halad, hanem egyik helyről a másikra. A puszta helyek egymás mellé sorakoztatva alkotják a teret. (A fogalmazás anakronisztikus, de az öntudatlan szemléletnek megfelel.) Le is rajzolhatjuk, egy dimenzióra szorítkozva (1. ábra). Az idő békésen telik minden egyes puszta hely fölött, minden helyen egyformán. Egészítsük ki a "tér" ábráját úgy, hogy az idő múlását is feltüntetjük! Az időbeli kiterjedés ábrázolására a papír függőleges irányát, kiterjedését használhatjuk fel (2. ábra). A "puszta helyeknek" és a fölöttük telő időnek ezen a milliméterpapír-szerű "térképén" jelennek meg az anyagi folyamatok, a testek mozgásai. A 3. ábrán két test sorsát tüntettük fel vastag vonallal. Egyikük mindvégig nyugalombanvan, másikuk helyét sorozatosan változtatva mozog. Látnivaló, hogy ebben a képben a mozgás alapvetően más, mint a nyugalom, nem sima, hanem "aggasztóan érdes" vonal ábrázolja.

2. ábra (balra). Az idő múlása.
3. ábra. Nyugalom és mozgás
A görög bölcselők (persze, grafikus ábrázolás nélkül) bátran szembenéztek saját tér- és időfogalmuk e nehézségével. "Egy tárgy vagy abban a pontban mozoghat, ahol van, vagy abban a pontban, ahol nincs. Abban a pontban, ahol van, nem mozoghat, mert abban a pillanatban, amikor ott van, áll, és ami áll, az nem mozog. Továbbá abban a pontban, ahol nincs, újból nem mozoghat, mert ahol nem létezik, ott semmiféle hatást nem gyakorolhat. Meggondolásaimból következik, hogy egyetlen test sem mozog" - vallja Diodórosz, mérsékelten imponálva az utókor diákjainak.
Ami az újkori fizika kibontakozását illeti, a szemlélet és a magyarázatkeresés birkózása végigkíséri a klasszikus fizikát is.
"Newton szerint a fény részecskékből áll, de Huygens azt mondta, hogy a fény hullám" - fújjuk a leckét az iskolában. Pedig Newton meghatározta a különböző színekhez tartozó hullámhosszakat! (A szó használatát azonban elkerülte.) "Az iránt, hogy a mennyet folyékony közegek töltik meg, … igen nagy kétely merül fel…" - írta, az égi mozgások súrlódásmentességére utalva. A XIX. század végéig sem derült ki, hogy ha a tünékeny, keletkezni és elenyészni képes fény nem az éterrészecskék rezgésének tovaterjedése, akkor micsoda. (Ha viszont éterrezgés, akkor az éternek - a fénypolarizációval kapcsolatban - a szilárd testek tulajdonságaival kell bírnia!) A példák számát szaporíthatnánk.
Így hát abban is van igazság, hogy a letűnt korok "keserves" dilemmáit halványan érezzük át. Mindenesetre a XIX. század fizikusainak önelégültsége mögött nem "puszta igénytelenség" rejlik, hanem - Darwin eszméinek megfoganása előtt! - inkább kényszerű belenyugvás abba a kanti tanításba, hogy elménk a világot csak a priori szemléleti formákon keresztül képes megközelíteni, a "Ding an sich" ("magánvaló") ismeretlen marad. Az a priori trónfosztása csupán a fizika forradalmához vezető új kísérleti tények nyomására ment végbe.
A téridő
Fogalmak magasabb rendű egységbe tömörülésére a legszebb példa a tér+idő= =téridő metamorfózis. És ha már egyszer a fizika évét éppen a speciális relativitáselmélet századik születésnapja tünteti ki, talán nem ünneprontó akadékoskodás, ha a megemlékezés kényelmesen süppedő foteljét egy kis időre bütykös iskolapadra cseréljük, és vázlatosan, de érdemben végigmegyünk ennek a fogalomgazdagodásnak az útján.
Első nekifutásra mindössze arról van szó, hogy a különböző tárgyak, történések térbeli és időbeli kiterjedését nem egymástól elszigetelten, hanem egyszerre, együtt kell vizsgálni. Konkrétabban: a geometriai elnevezéseket (pont, vonal, egyenes stb.) nem annyira a tárgyak térbeli, mint inkább a folyamatok tér- és időbeli viszonyaira kell alkalmazni. Példa: egy ottfelejtett krétapötty a táblán az új szóhasználat szerint nem pont, hanem vonal, mert az időbeli kiterjedése nagy. Pont is van a téridőn, így hívjuk a - térben és időben egyaránt lokalizált - eseményt.
A 2. vagy a 3. ábra tulajdonképpen nem egyéb, mint egy kétdimenziós téridő (egy térbeli + egy időbeli dimenzió) ábrázolása a papír síkján, azzal megterhelve, hogy a puszta helyeknek önálló, tartósan azonosítható létet, sorsot tulajdonítunk. És még valamivel megterhelve.
A 2. ábrán a (vízszintes) "gyöngysor" a puszta helyeket jelenti "egy adott pillanatban". Honnan vesszük, hogy az idő máshol is ugyanúgy telik, mint ott, ahol éppen mi vagyunk? Természetesen a tapasztalatból. Ha elmélyedten ülünk és egyszer csak felpillantunk, akkor mindazt láthatjuk, egyszerre, ami "abban a pillanatban" közel és távol történik. Ne szégyelljük bevallani, hogy hallgatólagosan valami Platón "látósugár-elméletéhez" hasonló él bennünk, hiszen ma is nyugodtan mondjuk, hogy "ráesik a pillantásunk" vagy "rávetjük a pillantásunkat" valamire. És igenis ma is úgy érezzük, hogy akire rápillantunk, azt azonnal látjuk. Persze, világos, hogy a fény hoz hírt az eseményekről, de öntudatlan szemléletünk ma is az, hogy ez a híradás "nem fogyaszt időt". Ezért természetesnek tartjuk, hogy mindazt, ami a világban történik, egymás után következő "Most!"-ok sorozatával írhatjuk le; egy-egy "Most!" a tér, illetve a benne lévő testek állapotát veszi számba abban a pillanatban.
Hiába tudjuk Römer Olaf óta, hogy a fény véges sebességgel terjed, távoli, evolúciós múltunk során (sokak szerint különösen a dinoszauruszok korában) a bennünket körülvevő történések idő szerinti rendezése olyan gyümölcsöző volt, hogy idegrendszerünk erre a koncepcióra alapuló keretet épített ki magának, így rögzült szemléletünkben az egyetemes, mindenütt egyformán telő idő képzete. Közömbösen vesszük tudomásul, hogy a fénysebesség véges, és természetesnek véljük, hogy az egy ("igazi") "Most!"-hoz tartozó eseményeket egy végtelenül gyors, időt csakugyan nem fogyasztó jel kapcsolná egymáshoz, és hogy két távoli esemény egyidejűsége akkor is értelmes fogalom, ha ilyen jel nincs, tehát az egyidejűséget közvetlenül, egyetlen jel kibocsátásával nem tudjuk ellenőrizni. (Amikor Newton a mozgástörvények szabatos megfogalmazása érdekében bevezette az abszolút idő fogalmát, csak azt mondta ki határozottan, ami homályosan mindenkiben élt. Kant, nem bírván megküzdeni a newtoni tanítás tekintélyével, a minden anyagi folyamattól függetlenül telő abszolút idő fogalmát, melynek "kísérteties" jellegét jól látta, a priori kategória rangjára emelte.)

4. ábra. Két űrhajó sorsa a téridőben
Képzeljünk el mármost két egymáshoz képest mozgó űrhajót, úgy, ahogy talán Verne Gyula álmodhatta volna meg őket a XIX. században. A 4. ábrán a két űrhajó sorsát láthatjuk. Mindkét űrhajó szabadon siklik (vagy "lebeg") az űrben (pontosabban az éterben, hiszen Verne korában vagyunk), távol a nagy tömegektől. Az O pontban (téridőpontban) találkoztak, azóta távolodnak egymástól.
Az a űrhajó kapitánya - nevezzük Alexnek, hogy ne mindig Aliz legyen -, aki szeretne bepillantást nyerni a b kapitány - mondjuk Bea - életébe, valamely A’ téridőpontban radarjelet indít Bea felé, amely a B eseményről hírt hozva az A’’ pontban ér vissza. Azt az A eseményt Alex életében, amely B-vel pontosan egyidejű, egy végtelenül gyors jel segítségével lehetne könnyen azonosítani De tegyük fel, Alex tudja valahonnan, hogy az ő űrhajója éppen áll az éterben. Akkor könnyen megtalálja a B-vel egyidejű A-t végtelenül gyors jel nélkül is. A nyilván felezi az A’A’’ időközt, hiszen a nyugvó éterben a fény utazása oda és vissza ugyanannyi ideig tart.
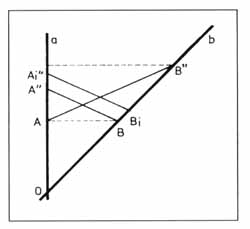
5. ábra. Ki van nyugalomban?
Ha netán Bea is azt hiszi, hogy az ő űrhajója áll az éterben és vitázni kezdenek (a diskurához szükséges radarjeleket már nem rajzoltuk be), Alexnek "könnyű a dolga" (5. ábra). Tegyük fel, hogy véletlenségből (hisz még nem tudott az A’’ eseményről) az A pontban is elindított egy radarjelet Bea felé, ez a B’’ pontban érkezik meg Beához. Nos, Alexnek elég, ha megtudakolja, mennyi idő telt el Bea űrhajójában B és B’’ között. Az olvasó is hasonlítsa össze az 5. ábrán a két szaggatott vonal, illetve A és A’’ egymástól való távolságát.
Látnivaló, hogy ha egyszer A és B egyidejű, azaz a találkozás óta eltelt OB időtartam a b űrhajóban ugyanakkora, mint az OA időtartam az a űrhajóban, továbbá Alex nyugszik, Bea pedig mozog (távolodik) az éterben, akkor az AB’’, illetve BA’’ fényjelek cseréjével kapott AA’’ és BB’’ időtartamok közül BB’’ a nagyobb.
Eddig mindössze annyit tettünk, hogy a térbeli és időbeli kiterjedést együtt ábrázoltuk. A két dimenzió önálló maradt: az idő mindenütt egységesen, a rajzon függőleges irányban telik, egymást követő "Most!"-okra szeletelve a világot.
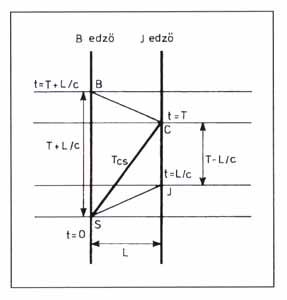
6. ábra. Csilla esete a két edzővel
Most ugrik a majom a vízbe! (Illetve egy úszócsillag.) A fogalmi gazdagodás egy váratlan kísérleti eredmény nyomán következett be. Ezt a kísérletet most "az ifjúság számára átdolgozott" formában mutatjuk be. A történet, amit kerítünk hozzá, gyermetegen mesterkélt, de annál kifejezőbb. A 6. ábrán a két függőleges egyenes két edző világvonala (sorsa), akik egy úszómedence bal, illetve jobb szélén állnak, stopperrel a kezükben. A tört vonal egy úszócsillag, mondjuk, Csilla "történetét" mutatja. S jelöli a start eseményét, amikor Csilla beugrik a vízbe, C a célba érés eseménye, az L hosszúságú medence túlsó szélén.
A jobb oldali edző akkor indítja a stopperét (J esemény), amikor látja, hogy Csilla elindul. A J esemény egy kicsit későbbi, mint az S tényleges indulás, hiszen a fénynek is kell egy kevés (L/c nagyságú) idő, amíg átér a medencén. (Csilla már olyan jól úszik, hogy az ilyen kis időtartamok is számítanak.) A C pont a J edző stopperének megállítását is jelenti. (Itt nincs időkésés, hiszen a célba érés az edző szeme előtt történik.) Látnivaló, hogy a J edző az úszás valódi, T időtartama helyett TJ=T-L/c időtartamot mér. Kompenzációképpen a B edző is méri az időt. Akkor indítja a stopperét, amikor (az orra előtt) Csilla beugrik a vízbe, és akkor állítja meg, amikor látja, kis késéssel, hogy Csilla célba ér (B esemény). Ő tehát TB=T+L/c időtartamot mér. A valódi időtartam nyilvánvalóan a két adat számtani közepe: T=(TB+TJ)/2.
Nyilvánvalóan? Tegyük fel, hogy Csilla ellenőrizni akarja az edzőket, és a titokban magával vitt óráról ő maga leolvassa, hogy mennyi ideig úszott. Döbbenten fogja megállapítani, hogy a saját maga által mért TCSidőtartam az edzők által közölt TB-nek és TJ-nek nem a számtani, hanem a mértani közepével egyezik meg!! Íme, a váratlan tapasztalat!
Két mennyiség mértani közepe kisebb, mint a számtani közepe (kivéve, ha a két mennyiség egyenlő, de esetünkben TB>TJ). Tehát TCS=Ö------TB·TJ<T=(TB+TJ)/2. Csilla saját ideje kisebb annál, amit az edzők állapítanak meg.
Ennek a tapasztalati ténynek (a ténylegesen elvégzett kísérleteket "Csilla esete a két edzővel" hűen tükrözi) az egyik folyománya, hogy - az 5. ábrára visszapillantva - köddé válik Alex magabiztossága, miszerint "ő nyugszik az éterben".
Az a Bi esemény (Bi="igazi" B), amely Bea életében ugyanolyan időbeli távolságra van O-tól, mint az A esemény Alex életében (OA=OBi), az 5. ábrán kissé feljebb csúszik. Összehasonlítani az A-ból, illetve Bi-ből indított fényjelek révén kapott BiB’’, illetve AAi’’ időtartamokat kell. Mint az olvasó maga is utánaszámolhat, Bea pontosan ugyanakkora (és nem nagyobb) BiB’’ időtartamról fog Alexnek beszámolni, mint amekkora az Alex által mért AAi’’ időtartam. Mindkettő egyforma joggal állíthatja, hogy ő van nyugalomban. A sebesség az éterhez képest üres fogalommá válik.
Másrészt kiderül, hogy a történésektől teljesen független, egyetemes idő nem is létezik. Az a kérdés, hogy két esemény - például a 6. ábrán S és C - között mekkora az időkülönbség, túl egyszerű: a válasz nemcsak attól függ, hogy melyik két eseményről van szó, hanem attól is, hogy milyen fizikai folyamatot képzelünk a két esemény közé. (Ha Csilla előbb lassan, majd nagyon gyorsan úszva jutna el S-től C-ig, sajátideje megint más - még kisebb - lenne.) Az új tényállás emlékeztet arra, amit a "közönséges" geometriában természetesnek tekintünk: ha elautózunk a barátunkhoz, a benzinköltség nemcsak attól függ, hogy ő hol lakik és mi hol lakunk, hanem attól is, hogy milyen útvonalat választunk. Mindezt röviden így fejezzük ki: a tér és az idő szerves geometriai egységet alkot. A könnyebb áttekintés kedvéért szerkeszthetünk ugyan (önkényesen) koordinátavonalakat a téridőre (ilyenek az 5. ábrán a szaggatott vonalak, vagy a 6. ábrán a t=0, t=L/c stb. jelű vonalak), de "a priori" a téridő nem esik szét "Most!"-okra.
Miért nem derült ki mindez korábban? Válasz: a 6. ábrán a TB és TJ időtartamok "a gyakorlatban" közel egyenlők. Akkor pedig a geometriai közép "csak észrevehetetlen mértékben" tér el a számtani középtől.
Epilógus
Az elmondottak éppen csak ízelítőt nyújtanak abból, hogyan válhat élménnyé egy átfogó, de szemléletellenes fogalom megszületése. Azt pedig csak "bizonyítás nélkül" jelenthetjük ki, hogy ha egyszer az új, "magasabb rendű" koncepció kialakult, akkor önálló életet kezd élni és"saját belső tartalékaira (is) támaszkodva" fejlődik tovább. A téridő fogalma mindenekelőtt szinte egy csapásra egy akolba terelte az anyag, energia, impulzus addig csonkán összefüggő, alapvető aspektusait. Azután helyet csinált a gravitáció (legendás kísérletekkel igazolt) modern elméletének. (Egy csíkokra szabdalt téridővel "nincs mit kezdeni," de ha a téridő összefüggő "lepedő", akkor lehet görbült is.) Innen a kozmológián át az ősrobbanáshoz vezetett az út, az akkori "forróság" a nagyenergiájú fizikával teremt kapcsolatot. "Kézenfekvő" lehetőség, hogy mikroszkopikus méretekben - ahová nem látunk - a téridő dimenziószáma nem négy, hanem nagyobb.
Új mítosz, "matematikai
mese" van alakulóban, mindent ígér, akár az ősiek. A kutatókat olykor
megrészegíti, de a mítosznak az az átélése, ami eleinket olyan szívderítően
jellemezte, a többségtől elvétetett. Ez bizony kiűzetés a paradicsomból!
- Az oktatásügyre nagy felelősség hárul. Mind az iskolai fizika kivégzése,
mind a "túl elvontnak, amit az ördög sem ért," az erőltetése
bűn. Mind a kettő kiszolgáltatottságra és elidegenedésre
vezet. Nem a változó körülményekhez való gyors, de vak alkalmazkodás
gyakorlása az iskola feladata, nem az segít szembenézni a jövő kihívásaival,
hanem - kísérlet és elmélet mértéktartó párosításával - annak az
élménnyé tétele, hogy a fizika s általában a természettudomány a
jelenségeket érthetőbbé, nem pedig érthetetlenebbé teszi.
| Természet Világa, | 136. évfolyam,
3. szám, 2005. március http://www.termeszetvilaga.hu/ http://www.chemonet.hu/TermVil/ |