Entrópia, biliárdok, whisky szódával és Abel-díj
Ismét komoly öröm érte a magyar matematikai közösséget: Jakov Szinaj (Yakov Sinai), sokunk tanítómestere és barátja Abel-díjat kapott! A díjat 2003 óta évente adományozza a Norvég Tudományos Akadémia a matematika területén elért kimagasló életmű jutalmaként. A díj névadója Niels Henrik Abel norvég matematikus (1802–1829).1

Jakov Grigorjevics Szinaj
(Kredit:Knut Falch)
Én is alkalmazom a Lovász László által Szemerédi Endre Abel-díja alkalmából írott cikkében megvalósított módszert: idézem a díjbizottság indokolását és alkalmakként kiegészítésekkel, magyarázatokkal látom el.
„A Norvég Tudományos Akadémia (Norwegian Academy of Science and Letters) úgy határozott, hogy 2014-ben Abel-díjjal tünteti ki Yakov G. Sinai-t (a Princeton University és az Orosz Tudományos Akadémia Landau Elméleti Fizika Intézetének professzorát) a dinamikai rendszerek elmélete, az ergodelmélet és a matematikai fizika területén elért alapvető eredményeiért.”
„Newton óta matematikusok, természettudósok és mérnökök egyaránt használják a differenciálegyenleteket természeti jelenségek magyarázatára és ezek fejlődésének jóslására. Számos egyenlet sztochasztikus tagokat is tartalmaz, hogy ismeretlen – alkalmakként véletlen – tényezőket is figyelembe vehessen, amelyek szintén befolyásolják a fejlődést. A determinisztikus és sztochasztikus fejlődési egyenletek olyan egészen különböző jelenségeket írnak le, mint a bolygómozgás, az óceánok áramlása, a pszichológiai ciklusok, a populációdinamika és az elektromos hálózatok, hogy csak néhányat említsünk. Ezen jelenségek közül egyesek nagy pontossággal előre jelezhetőek, mások kaotikus, előre nem jelezhető módon fejlődnek. Mára világossá vált, hogy a rend és a káosz szorosan összefüggenek: kaotikus mozgást figyelhetünk meg determinisztikus rendszerekben, és megfordítva a kaotikus rendszerek statisztikai analízise határozott előrejelzésekhez vezethet.”
Az ergodelmélet a XX. század 30-as éveinek elejére jött létre a determinisztikus rendszerekben fellépő véletlen viselkedés mélyebb megértése céljából. A fő motiváció a XIX. században kialakult statisztikus fizika érveléseinek matematikailag pontos megértése volt. Ennek fontosságára már Hilbert is felhívta a matematikusok figyelmét nevezetes problémái közül a 6.-ban (ennek ezt a címet adta: a Fizika Axiómáinak Matematikai Megalapozása). Valóban, a statisztikus fizikának az iskolában is tanult fogalmai makroszkopikus fogalmak: hátterükben az a gondolat van, hogy pl. a hőmérséklet, a nyomás egy gáz vagy folyadék nagyszámú részecskéi kollektív viselkedésének eredménye. Mai nyelven azt mondanánk, hogy ezek a fogalmak a newtoni fizika mikroszkopikus, determinisztikus, differenciálegyenletekkel leírható törvényei szerint mozgó rendszerekben érvényes nagy számok törvényének kifejezései.
Az 1960-as évek két tekintetben hoztak, mondhatni, forradalmi fejlődést. Egyrészt a dinamikai rendszerek elméletén belül kialakult és megerősödött – elsősorban Anoszov, Szinaj és Smale (Fields Érem, 1966) munkásságának eredményeként – az ún. sima, azaz differenciálhatóan fejlődő hiperbolikus rendszerek elmélete. Ezek messzemenő általánosításai a Bolyai–Lobacsevszkij-geometriában megfigyelt és leírt egyenletes mozgásnak. Ott a hiperbolikus viselkedés (bizonyos irányokban nyújtás, bizonyos irányokban összehúzás) eredményezi a véletlen viselkedést. Másrészt akkor a számítógépek már képesek voltak bonyolult jelenségek, mint pl. az aero-, ill. a hidrodinamika egyenletei (Navier–Stokes- egyenlet) megoldásának számolására (pontosabban az egyenletek erősen leegyszerűsített változatainak numerikus megoldására). Kiderült, hogy már egyszerű nemlineáris differenciálegyenletek megoldásai is tudnak kaotikusan viselkedni, pl. érmével való dobások sorozatát is előállítani.
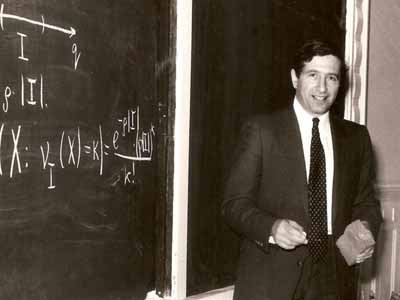
Előadása az MTA Matematikai Kutatóintézetében, 1985. január 30-án
„Jakov Szinaj alapvető eredményeket ért el ezen a széles kutatási területen. Meglepő kapcsolatokat fedezett fel rend és káosz között és továbbfejlesztette a valószínűségi és mértékelméleti módszerek alkalmazását a dinamikai rendszerek elméletében. Megtermékenyítő eredményei vannak az ergodelméletben, amely a rendszerek azon viselkedését tanulmányozza, hogy azok az összes lehetséges állapotaikat felkeressék bizonyos statisztika szerint. Ugyancsak kiemelkedő eredményei vannak a statisztikus fizikában, amely nagyon sok részecskéből álló rendszerek, mint pl. egy gáz molekulái, viselkedését írja le.”
Szinaj egy kimagasló jelentőségű kutatása lehetővé tette, hogy az említett hiperbolikus dinamikai rendszerekkel izomorf ún. szimbolikus dinamikákat találjanak. Ezek előnye, hogy bár a szimbolikus rendszer általában nem Markov-lánc, de hatékonyan közelíthető Markov-láncokkal. Ezáltal lehetővé válik, hogy az eredeti dinamikai rendszer statisztikai tulajdonságainak leírására felhasználjuk a valószínűség-számítás eredményeit, módszereit, illetve a statisztikus fizika gondolatait. A különösen nagy matematikusok egyik jellemzője éppen az, hogy utakat vesznek észre, hidakat találnak a legkülönbözőbb területek között. Itt éppen ez történt.
„Szinaj egyik kiemelkedő eredménye, ezt egyébként Kolmogorov inspirálta, dinamikai rendszerek fontos invariánsát vezette be. Ez az invariáns Kolmogorov–Szinaj-entrópia néven vált ismertté. Rendszerek komplexitását méri trajektóriáinak mértékelméleti leírása alapján. Különösen fontos eredményekhez vezetett dinamikai rendszerek osztályozása kapcsán.”
Az entrópiára vonatkozó eredményét Szinaj 24 éves korában érte el. Itt is az információelméletben, termodinamikában illetve a dinamikai rendszerek elméletében találtak közös fogalmat, ezúttal Kolmogorovval közösen. Érdekességként jegyzem meg, hogy e munkát matematikusok, fizikusok különösen széles köre ismeri és használja. Ezek közül, akik először látták Szinajt, mindig meglepődtek: e klasszikus, ‚szakállas’ eredmény alapján sokkal idősebb tudósra számítottak (Szinaj 1935-ben született).
„Az ergodelméletnek is vezéregyénisége volt. A legelső eredményeket igazolta szóró biliárdok ergodicitására vonatkozólag Boltzmann szellemében, majd e munkát Bunimoviccsal és Csernovval folytatta. Markov felbontásokat konstruált Anoszov diffeomorfizmusok iterációira; ez kiemelkedő eredményekhez vezetett keverő rendszerek különböző osztályainak szimbolikus sorozatokkal való leírásában.”
A XIX. század statisztikus fizikájának vezéregyéniségei: Boltzmann, Gibbs, Maxwell hittek az atomelméletben, amely még a XX. század legelején sem volt általánosan elfogadott. Elméleteiket éppen az atomelmélet alapján dolgozták ki. Nevezetesen Boltzmann megfogalmazott és használt egy ún. ergodikus hipotézist, amely lényegében épp arról szólt, hogy egyensúlyban levő nagy részecskerendszerben, pl. egy edényben levő gázban valamilyen értelemben érvényes a nagy számok törvénye. Nála ennek a sejtésnek a megfogalmazása sem volt még matematikailag pontos. Már említettem, hogy a 1930-as évek elején kialakult az ergodelmélet és – jelentős részben éppen Neumann János ergodtételének következményeként – világossá vált, hogy mi is az az ergodicitás. Szinaj 1962-ben megfogalmazta Boltzmann ergodikus hipotézisének egy konkrét, igen erős változatát: a D-dimenziós tóruszon adott N kemény golyó rugalmasan ütköző rendszere ergodikus, azaz érvényes rá a nagy számok törvénye (itt D = 2, 3, …; N = 2, 3, …). Ezt nevezzük ma Boltzmann–Szinaj-ergodikus hipotézisnek. A figyelmes olvasó már nyilván észrevette, hogy – Boltzmann hipotézisével ellentétben – itt fix rendszerekről van szó: nem szükséges a részecskék számával végtelenhez tartani.

Szinaj bizonyításának
alapgondolata egy söralátéten
(Krámli András archívumából)
Szinajnak 1970-re sikerült a hipotézist az N=D=2 esetre igazolnia, azaz megmutatta, hogy a kétdimenziós tóruszon mozgó, rugalmasan ütköző, két kemény korongból álló rendszer ergodikus. Bizonyításának kiindulópontja az volt, hogy ez a rendszer olyan biliárd, ún. Szinaj-biliárd, ahol a szórótestek szigorúan konvexek. A bizonyításhoz a sima, hiperbolikus dinamikai rendszerek elméletét (mint említettem, ezt a 60-as évek elején dolgozták ki) kellett kiterjesztenie szakadásokkal rendelkező hiperbolikus dinamikai rendszerekre. Ez a jelentéktelennek tűnő apró továbblépés igen komoly kreativitást és mély technikák megalkotását követelte. (A részletek iránt is érdeklődő olvasónak javasolom a Természet Világa Matematika különszámában 1998-ban megjelent, erről szóló cikkemet.) További 17 év múlva Csernovval közösen sikerült az előbbi eredményt tetszőleges dimenzióra is igazolniuk: a D-dimenziós tóruszon mozgó, rugalmasan ütköző két kemény golyó rendszere ergodikus.2
Érdemes külön szólnom Szinaj Bunimoviccsal és Csernovval közös munkájáról. Einstein 1905-ben – az anyag atomos elméletét feltételezve – fizikai gondolatmenettel levezette a diffúziós egyenletet folyadékban oldott parányi részecske kaotikus, ún. Brown-mozgására. (Ezt Robert Brown angol botanikus figyelte meg először 1827-ben az akkor már elég erős mikroszkóp segítségével.) Einstein ugyanitt pontosan is kiszámolta az Avogadro-számot. Elméleti eredményét Jean Baptiste Perrin francia kísérleti fizikus 1908-ban experimentálisan is igazolta. Igazából ezzel vált az atomelmélet bizonyított tudományos elméletté, és ezért méltán kapott Perrin Nobel díjat 1926-ban. Einstein levezetése erősen heurisztikus volt, és később számos modell született a Brown-mozgás mikroszkopikus feltételekből való matematikailag is teljes levezetésére.

Szinaj átveszi az Abel-díjat Haakon norvég trónörököstől (Kredit: NTB/Scanpix)
Szinaj 1981-ben Bunimoviccsal, majd 1991-ben kiegészülve Csernovval is, Hendrik Aanton Lorentz Nobel-díjas holland fizikus 1905-ben talált modelljéhez tért vissza.3
Lorentz igazából kristályban mozgó klasszikus elektron mozgását kívánta így modellezni. Tekintsünk a síkban szigorúan konvex szórótestek között mozgó pontszerű biliárdrészecskét, azaz a mozgás egyenletes és a szórótestekkel való ütközés rugalmas: beesési szög = visszaverődési szög. Itt tehát a dinamika determinisztikus, csak a kiinduló pont véletlen. Szinajék azt igazolták, hogy elég sűrű periodikus szórótest konfiguráció esetén ez a determinisztikus mozgás megfelelő skálázással (azaz eléggé messziről nézve) Brown–mozgás, pontosabban a valószínűség számítás nyelvén Wiener-folyamat. Tehát a Lorentz- folyamat ugyanúgy viselkedik, mint egy véletlen bolyongás; ez utóbbit éppen a Brown-mozgás sztochasztikus modelljének tekinthetjük.4
E téma befejezéséül megjegyzem, hogy a bizonyítások technikája Szinaj fentebb már említett gondolatán alapul: a Lorentz-folyamat helyett vele izomorf – bizonyos értelemben közel-Markov – szimbolikus sorozatokat vezetnek be.

Az „Abel-előadók” 2014-ben.
Balról: Grigorij Margulisz, Szász Domokos, Konsztantyin Khanin és Jakov
Szinaj (Az előadásokról készült videók elérhetők az Abel-díj honlapján:
https://www.abelprize.no/artikkel/vis.html?tid=61307)
(Kredit: Eirik Furu)
„Ruelle-lel és Bowennel párhuzamosan felfedezte az ún. SRB-mértékeket: ezek meglehetősen általános és különleges szerepet játszó, időben invariáns mértékek kaotikus disszipatív rendszerek esetén. Ez a rugalmas fogalom igen hasznos lett alapvető dinamikai rendszerek kvalitatív tanulmányozásában, valamint olyan reális jelenségek, mint a turbulencia megértésében.”
A newtoni rendszerekben az energia megmarad, és a klasszikus ergodelmélet eredményei éppen ilyen rendszerekre voltak érvényesek. Számos rendkívül érdekes fizikai jelenség van, ahol az energia csökken, disszipálódik. (Az ilyen rendszerek aszimptotikusan fraktálokon élnek, amelyek rendkívül izgalmas matematikai és természeti jelenségek, objektumok.) Az SRB-mértéknek az ilyen jelenségeknél van alapvető szerepe, például ennek segítségével ilyen rendszereknél is megfogalmazhatók ergodikus tételek, és így értelmezhető a statisztikus viselkedés is.
„Más úttörő jelentőségű munkái a matematikai fizika területén: véletlen közegű bolyongások (Szinaj-bolyongás), fázisátmenetek (Pirogov–Szinaj-elmélet), egy-dimenziós turbulencia (a sztochasztikus Burgers-egyenlet statisztikus sokk-struktúrájának leírása, E-Khanin-Mazel-Szinaj), a renorm csoport módszer (Bleher–Szinaj), diszkrét Schrödinger-operátorok spektruma.”
Ezekről az eredményekről egyenként is sokat kellene írni, így csak apróbb megjegyzéseket teszek. A Szinaj-bolyongásról szóló dolgozata 1982-ben jelent meg. Szinaj az Abel-díjat megköszönő beszédében külön kitért a Landau Elméleti Fizikai Intézetben eltöltött éveire, az ott kialakított kutatói stílusra. Matematikusok és fizikusok mes.szemenően tisztelték egymást, igen kiváló társaság volt ott egyébként is. Megtanultak egymás nyelvén beszélni, egymást megérteni. Rendszeresen voltak közös szemináriumaik. Magam is azt láttam moszkvai látogatásaimon, hogy Szinaj rendszeresen találkozott fizikusokkal, meghallgatta őket, jegyzetelt, gondolkodott a problémáikon, kérdéseiken. Valóban, sokszor a fizikusok a matematikusoknál hamarabb felfedeznek, szimulálnak érdekes jelenségeket, ezekre érdemes odafigyelni. Az egydimenziós véletlen közegű bolyongásnak a szokásos véletlen bolyongástól erősen eltérő viselkedését is fizikusok vették észre. Szinajnak az adott esetben megvolt a matematikai ereje, eszköztára, hogy ténylegesen igazolja is ennek a bolyongásnak a radikális lelassulását. Érdekességként mondom el, hogy 1982-ben Krámli Andrással meglátogattuk Szinajt, aki akkor egy hónapot töltött Lipcsében. Ott a Goethe által a Faustban is felidézett Auerbachs Kellerben egy söralátéten mondta el nekünk a bizonyítás alapgondolatát, Krámlinak az alátét még ma is megvan.
A fázisátmenetek, pl. a mágnesesség kialakulása az egyensúlyi statisztikus fizika alapvető kérdése. Az ezt megvilágító Pirogov–Szinaj-elmélet ma is a fizikai kép alapja. Amikor Szinaj ezzel foglalkozott intenzíven, a whiskys pohárban is a fázisátmenetet látta: a szilárd állapotú jég, a cseppfolyós whisky, a légnemű buborékok egyszerre mutatják mindhárom halmazállapotot, nem beszélve a poháron kicsapódó páráról. A renorm-csoport módszerrel kapcsolatban megjegyzem, hogy ennek fizikai kidolgozásáért 1982-ben K. G. Wilson Nobel-díjat kapott. Szinaj a módszer matematikailag szigorú – a nemlineáris funkcionálanalízisen alapuló – megalapozását adta Bleherrel Freeman Dyson hierarchikus modelljére. Kutatásukat később egyrészt Major Péter – számos, Bleherrel közös, finom analízist igénylő munkában – folytatta, másrészt a módszer a dinamikai rendszerek elméletében is alapvető és igen sikeres lett (Feigenbaum-univerzalitás igazolása).
„Szinaj vezető matematikusok generációit nevelte ki, illetve befolyásolta kutatási területein. Számos módszere, eredménye matematikai fizikusok mindennapos eszköztárába került. Kutatásainak széles és mély hatásuk van a matematikára és a fizikára, valamint e területek folyamatos együttműködésére is.”
Szinajnak mintegy 60–70 közvetlen tanítványa van, jóllehet 1971 és 1993 között csak félállásban volt egyetemen. Tanítványa volt többek között G. Margulisz Fields-érmes és Wolf-díjas matematikus, Marina Ratner, aki, akárcsak Margulisz, tagja az USA National Academy of Sciences-nek, Anatole Katok, az American Academy of Arts and Sciences tagja. Jelentős azoknak a száma is, akik nem voltak közvetlen tanítványai, Magyarországon kívül különösen sokan vannak ilyenek Olaszországban és voltak Lengyelországban. Szinaj 1993-ban lett az MTA tiszteleti tagja, 2002-ben a BME tiszteleti doktora, 1985-ben nagysikerű Turán Pál Emlékelőadásokat tartott az MTA Matematikai Kutatóintézetében. Tavaly Budapesten a European Meeting of Statisticians záró előadását tartotta számelméletről, majd Szegeden vett részt a Krámli András 70. születésnapjára Szegeden tartott workshopon, ahol hidrodinamikáról beszélt.
Ajánlott irodalom (a Természet Világában megjelent írásokból)
Tél Tamás: Törtdimenziós
rendszerek: a fraktálok. Természet Világa, 1984. 3. szám;
Szász Domokos: Matematikai
biliárdok. Ergodicitás és káosz. Természet Világa, 1998. III., Matematika
különszáma;
Tél Tamás: A káosz természetrajza.
Természet Világa, 1998. 9. szám;
Tél Tamás–Gruiz Márton:
Mi a káosz? Természet Világa, 2002. 7. szám;
Krámli András: Káosz matematikusszemmel.
Természet Világa, 2004. 7. szám;
A Nagy Fehér Főnök. Beszélgetés
Jakov Grigorjevics Szinaj professzorral. (Staar Gyula interjúja.) Természet
Világa, 1985. 8. szám.
--------------------------------
1 Érdekességként jegyzem meg, hogy Bolyai János is 1802-ben született.
2 A több részecskére vonatkozó Boltzmann–Szinaj-hipotézis igazolását egyébként Krámli Andrással és Simányi Nándorral 1991-ben sikerült megkezdenünk az N = 3, D= 2, 3… esetekkel. Tetszőleges N és D esetére tipikus golyórendszerekre 1999-ben Simányival közösen hiperbolicitást igazoltunk, ez az egodicitás előszobája. Ezután Simányi Nándor számos finom cikkében egyre javította az eredményeket, míg egy 2013-as dolgozatában teljessé vált a Boltzmann–Szinaj hipotézisre adott bizonyítás.
3 Nekem ténylegesen ez a kutatása keltette fel érdeklődésemet Szinaj módszerei iránt. A Brown-mozgás dinamikai elméletén dolgoztam és 1979-ben Szinaj a Lukács uszoda napozóján mesélt nekem és Krámli Andrásnak a Lorentz-folyamatra elért akkor éppen friss eredményéről. Ennek hatására kezdtem biliárdokkal foglalkozni.
4 Ha a szórótest-konfiguráció nem elég sűrű, akkor a skálázás is különbözik: messzebbről kell nézni a Lorentz folyamatra, de itt is Wiener folyamat a limesz. Blehernek ezt az 1992-es sejtését 2007-ben igazoltuk Varjú Tamással.
| Természet Világa, | 145. évfolyam, 8. szám,
2014. augusztus
http//www.termvil.hu/ |