 Sir
Roger Penrose 1931. augusztus 8-án született Colchesterben
(Essex, Anglia).
Sir
Roger Penrose 1931. augusztus 8-án született Colchesterben
(Essex, Anglia).MATEMATIKA
A nagy csempézõ
Beszélgetés
Roger Penrose-zal, az Oxfordi Egyetem professzorával
 Sir
Roger Penrose 1931. augusztus 8-án született Colchesterben
(Essex, Anglia).
Sir
Roger Penrose 1931. augusztus 8-án született Colchesterben
(Essex, Anglia).
A Cambridge Egyetemen szerzett doktori fokozatot 1957-ben algebrai geometriából, majd angol és amerikai egyetemeken dolgozott. 1964 és 1973 között docens, majd az alkalmazott matematika professzora a londoni Birkbeck College-ban. 1973-tól az Oxfordi Egyetemen a Rouse-Ball matematikai katedra professzora. A jeles matematikust és kozmológust tudományos eredményei elismeréseként 1994-ben lovaggá ütötték.
1969-ben Stephen Hawkinggel közösen bebizonyította, hogy a fekete lyuk belsejében lévõ összes anyag egyetlen ponttá, egy szingularitássá húzódik össze, és e térbeli matematikai pontban az anyag zérus térfogatú és végtelen sûrûségû. Penrose és Hawking az általános relativitáselmélet terén végzett briliáns kutatásaikért 1988-ban fizikai Wolf-díjat kaptak. Az indoklás szerint: Munkájukkal nagyban hozzájárultak a Világegyetem keletkezésérõl és további sorsáról alkotott elképzeléseink kialakulásához.
Penrose kidolgozott egy módszert arra, hogy a fekete lyukat körülvevõ téridõ tartományt leképezze. Ez a leképezés, amelyet Penrose-diagramnak neveznek, lehetõvé teszi a fekete lyuk felé közeledõ objektumra ható gravitációs effektusok szemléletes ábrázolását.
Õ a tvisztorelmélet atyja. A tvisztorok a téridõ alapjául szolgáló magasabb dimenziós komplex térben mûködõ, absztrakt geometriai objektumok.
A császár új elméje (számítógépek, gondolkodás és fizika törvényei) címû híres könyve az Akadémiai Kiadó gondozásában 1993-ban magyarul is megjelent. Folyóiratunk augusztusi és szeptemberi számában Martin Gardner kétrészes cikkben mutatta be Roger Penrose-nak a sík nem periodikus csempézésének problémájára adott megoldását, melyet azóta róla neveztek el.
Roger Penrose május végén Budapestre látogatott. Az interjú akkor készült vele a Központi Fizikai Kutató Intézetben.
Könyvtáram jeles darabja az Ön gondolatébresztõ munkája, A császár új elméje. Könyvébõl is kitûnik, nemigen hisz az erõs mesterséges intelligencia apostolainak. Nemrégiben azonban egy váratlan esemény kissé felborzolta a kedélyeket. Az IBM Deep Blue számítógépe hatjátszmás párosmérkõzésen legyõzte a zseniális sakkvilágbajnokot, Garri Kaszparovot. Ezek szerint a császár mégsem meztelen?
A számítógép gyõzelme nem volt különleges esemény, bár megvallom, nem számítottam arra, hogy Kaszparov már most elveszít egy ilyen párosmérkõzést. Ennek ideje a vártnál hamarabb eljött. De nem hatott a meglepetés erejével, mivel tudtuk, a sakk olyan játék, amit számítógépekkel is lehet játszani. A számítógép pedig jóval elõbbre lát, sokkal több változatot kiszámol, mint az ember.
A Kaszparovot legyõzõ Deep Blue állítólag másodpercenként 200 millió lépést vizsgált meg és értékelt...
Számítógéppel elõre számolni sakklépéseket bizonyos szempontból hatékonyabb, ugyanakkor nem intelligens játék. A gép nem úgy játszik, mint az ember. Nem érti a sakkot, nem tudja, mit játszik, megmagyarázni sem képes azt.
Vannak állások, melyeknél gyakorlatilag minden sakkjátékos azonnal látja, hogy mi a jó lépés. A Deep Blue ilyenkor is hosszú számításokat végzett, melynek eredményeként egy-két esetben ostoba lépést tett. Olyan húzást, melyet az ember abban az esetben nem lépett volna meg. Mert pusztán számításokkal nem feltétlenül a helyes lépést választjuk. Egyszerûbb állásoknál tehát az ember mindig látja, hogy mit kell tennie, ugyanakkor az is nyilvánvaló, hogy a sok számítást követelõ bonyolultabb helyzetekben a gyorsan mûködõ számítógéppel elérhetõk bizonyos eredmények. A két dolog természetesen nem ugyanaz. Csupán számításokkal nem sokra mehetünk, mindenesetre, ha a lépések elemzésekor sok számítás történik, akkor eljuthatunk olyan szintre, ami már bizonyos emberi szintû megértést, intelligenciát feltételez.
Úgy gondolom, a világbajnok Kaszparov azért veszített a Deep Blue ellen, mert nyugtalan és izgatott volt. Idegesítette a szokatlan helyzet, kihozta a sodrából, elveszítette a hidegvérét. Az utolsó, mindent eldöntõ játszmában már a játék korai szakaszában tõle nem várt, megdöbbentõ és végzetes hibát követett el. Normál körülmények között mindez bizonyosan nem következett volna be. Meg tudom mutatni az állást.
Köszönöm, ismerem a részleteket. Kaszparov Caro-Cann védelmet választott és már a 6. lépésével belement egy rossz változatba. Magam is hosszú ideig aktívan sakkoztam, ezért sem közömbös számomra, hogy ki gyõz, a gép vagy az ember. Pontosabban fogalmazva: a gépkészítõ ember vagy a sakkjátékos.
Professzor úr, mit gondol, mindezt csak a számítógép gyorsasága teszi, vagy talán az itt a probléma, hogy a 8x8 mezõre szorított sakkjáték nem elég bonyolult rendszer ahhoz, hogy az emberi gondolkodás egyfajta modellje legyen?
A sakk véges játék, ezért bizonyos módon követhetõ számítástechnikai eszközökkel. Említettem már, hogy egyfajta egyensúly van a megértés és a számítás között. Miután a gép rövid idõ alatt igen nagy mennyiségû számítást képes elvégezni, ez bizonyos körülmények között jelentõs elõny lehet. Ugyanakkor önmagában ez még semmit nem mond, nem arra mutat, hogy a számítógép valamilyen tudattal, egyfajta gondolkodásmóddal rendelkezik. A gépnek, miközben a számításokat végzi, nincsenek emberi kvalitásai.
A gép után következzék az ember. Hogyan lett Ön matematikus? Tudjuk, jó családba született, hiszen édesapja a híres genetikus, L. S. Penrose. Milyen útravalót kapott a családi háztól?
Apámon kívül bátyám, Oliver is hatással volt rám. Atyám különösképpen szerette a matematikát, érdeklõdésem tõle ered. Gyakran beszélgetett velünk matematikáról, a természet dolgairól. Nem volt matematikus, de a matematikát felhasználta munkájában. Kisgyermekként elkészítettem különbözõ geometriai testek modelljét, matematikai rejtvényeken törtem a fejem és magam is igyekeztem kitalálni hasonlókat.
Emlékszem arra, amikor az iskolában elkezdtük tanulni a differenciál- és az integrálszámítást, eldicsekedtem vele apámnak. Õ erre azonnal elkezdte nekem magyarázni, mert attól tartott, hogy a tanárunk nem megfelelõen mondja el. Tehát érdekelte a matematika és szeretett róla beszélni.
Martin Gardner írja egy helyen, hogy Ön nagyon szereti a matematikai játékokat. E rajongásának elmondaná egy konkrét megnyilvánulási formáját?
Magam is kitaláltam egyfajta matematikával összefüggõ kártyajátékot és ennek egy titkosírás variációját. Elmondok egy játékot, mellyel még fiatalemberként leptem meg Martin Gardnert. Rögzítsük a spárga egyik végét. Ezután kössünk hurkokat a madzagra, egészen addig, míg az tele nem lesz csomóval. Amint az ember a szabad végén meghúzza a spárgát, a fonal kiegyenesedik, eltûnnek a csomók. Észrevettem, hogy mindez szimmetrikus, ugyanezt megtehetjük a spárga másik felével is. Martin Gardnerre nagy hatást gyakorolt ez a matematikai játék.
A holland grafikus, M. C. Escher képein élõlények egymásba kapcsolódó rajzai fedik le a síkot. Ezek a rajzok periodikus csempézések. Ön a hetvenes évek elején megmutatta, miként lehet nem periodikus csempézéssel beborítani a síkot. Nagyon érdekelne, miként jött rá a megoldásra, hogyan született meg a gondolata és mindez mit takar?
Jó nehezet kérdez.
A különbözõ ötletek más-más alkalommal születnek. Több fokozata, több stációja van a gondolkodásnak. Eredetileg az ún. periodikus csempézés iránt érdeklõdtem. A késõbb rólam elnevezett Penrose-féle csempék egyszerûen csak eszembe jutottak. Szórakoztam, játszadoztam vele és egyszer csak megvolt.
Az egész egy rajzzal kezdõdött, valamilyen levél fejlécén. A levélben egy szemináriumra vagy talán elõadásra invitáltak, régóta hevert asztalomon, válaszolnom kellett volna rá, de húztam, halasztottam a levélírást. Nap mint nap ránéztem a meghívóra, a londoni egyetem címere díszítette, benne egy ötszög.
Játszadozni kezdtem az ötszöggel, hogyan lehetne folytatni, nagyobb struktúrákat építeni belõle, megfelelõen egymáshoz illeszkedõ elrendezésben. Azt hiszem, valójában Kepler hatása alatt cselekedtem. Apámnak volt egy könyve, benne olyan képek, például ötszögek, amiket még Kepler rajzolt. Az ötszögekkel nagyon sok mindent csinálhat az ember. Amikor elkezdtem velük játszadozni, lehetséges, hogy ez az emlék dolgozott bennem. Rájöttem, Kepler is lényegében ilyenfajta lefedést igyekezett konstruálni, mint amit én tettem. Minden bizonnyal eljutott az enyémhez nagyon közelálló elrendezésekhez.
A síkbeli Penrose-világoknak mik a rejtett kincsei? Milyen matematikai és egyéb kérdésekre adott választ az Ön konstrukciója?
Nem állt szándékomban különleges problémát megoldani vagy valamiféle rejtett elvet feltárni. Egyszerûen csak eljátszottam ezekkel a csempeformákkal, mert ezt a foglalatosságot nagyon érdekesnek tartottam. Jó példája ez annak a matematikai kutatásnak, amikor az ember nem meghatározott céllal lát munkához, hanem a kíváncsiság, a kérdéskör iránti érdeklõdés hajtja. Korábban már létezett egy síkot lefedõ hat csempébõl álló halmaz, amit Rafael Robinson talált ki. Amikor rájöttem az ötszögekbõl álló szimmetrikus elrendezésre, melyet Kepler ábrája inspirált, azonnal elújságoltam azt az éppen kórházban fekvõ barátomnak. Akkor jöttem rá, hogy hat csempébõl álló rendszert tudok konstruálni, ahol mindegyik csempének más az alakja és kirakós játékként egymáshoz illeszthetõk. Megjelentettem a matematikai intézetek publikációjában, olyasmi címmel, hogy esztétika az alkalmazott matematikában. Ezután Princetonból Oxfordba látogatott Simon Coutching, aki elmesélte, Robinson azon dolgozik, hogy minél kevesebbre leszorítsa a különbözõ csempék számát. Eredetileg 25 000 körüli volt a sík lefedéséhez használt különbözõ csempék száma, majd 100, ezt sikerült Robinsonnak 6-ra csökkentenie.
Hamar rájöttem, miként lehet rendszeremben elég egyszerû mûvelettel ötre csökkenteni a csempék számát. Tovább gondolkoztam, majd négyre, a végén kettõre redukáltam a számukat. Ez már nem jelentett túl nagy munkát. A gondolkodás valójában próbálgatások sorozatából állt. Mindenesetre eljutottam a legkevesebb számú csempéhez, amivel a nem periodikus elrendezést kialakíthattam.
Robinson csempéit négyzetes szimmetria jellemezte, az enyéim rendelkeztek azzal a különleges tulajdonsággal, hogy megvolt bennük az ötszöges szimmetria. Ez az ötfogású szimmetria eddig ismeretlen volt a krisztallográfiában. Az általános tételek szerint ott csak kettõ-, három-, négy- és hatfogású szimmetriák voltak lehetségesek. Amennyiben az ember a tételt megkerüli, csak közelítõleg periodikus szimmetriát talál, így jön létre az ötfogású szimmetria.
Tíz év telhetett el csempéim felfedezése után, amikor Schechtman és munkatársai méréseik során bizonyos anyagoknál olyan spektrumokat figyeltek meg, melyek öt- vagy tízfogásos szimmetriával rendelkeztek. Ez az érdekes fejlemény nagy meglepetést okozott a kutatók között. Steinhardt és munkatársai ekkor azzal az elképzeléssel álltak elõ, hogy csempéimnek szerepük lehet az atomok elrendezésében. A. Mackay is ezt gondolta. Következõ lépésként a természetben elõforduló olyan anyagokat találtak, amelyek ilyen szimmetriát mutatnak. Manapság már mindezt általánosan elfogadják, sok kutató dolgozik ezen a területen. Igaz, akad pár szkeptikus is, de ez természetes. Jó, hogy vannak.
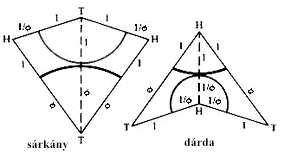 Az
Ön rendszerében két alakzattal, a dárdával
és a sárkánnyal készül a sík
nem periodikus lefedése. Elképzelhetõ, hogy létezik
egyetlen alakzat is, amellyel nem periodikusan csempézhetõ
a sík?
Az
Ön rendszerében két alakzattal, a dárdával
és a sárkánnyal készül a sík
nem periodikus lefedése. Elképzelhetõ, hogy létezik
egyetlen alakzat is, amellyel nem periodikusan csempézhetõ
a sík?
Abban a cikkben, amelyik legközelebb jutott ehhez a kérdéshez, a válasz attól függ, milyen szabályokat fogadunk el az illeszkedésre. Bizonyos szempontból a szabályok egy-egy extra csempével helyettesíthetõk. Amennyiben egymásba illõ csempéket követelünk meg, akkor legalább három ilyenre van szükségünk, de kettõre levihetjük a számukat.
Említette, hogy a kristálytanban meglepõ alkalmazásra talált a nem periodikus csempézése. Más tudományágakban, mondjuk a biológiában is jelentõsége lehet ennek?
Lehetséges, hiszen már Kepler is érdeklõdött az után, hogy elõfordul-e a természetben az ötfogásos szimmetria. Többen felvetették, vannak olyan vírusok, melyek ezzel a szimmetriával rendelkeznek. Találtak is mikroszkopikus élõ rendszereknél ilyen szimmetriát, de hogy ennek van-e valamilyen jelentõsége, az nem az én felségterületem, errõl nem szeretnék véleményt formálni. Ami az alkalmazásokat illeti, én csupán egyrõl tudok. Az egyik francia cég olyan teflonserpenyõt készített, melyet ötfogású szimmetriával rendelkezõ kvázikristályos anyaggal vontak be. Ezek a nem periodikus szerkezetû kvázikristályos anyagok különlegesen kemények, emellett igen jól vezetik a hõt, ezért azután kiválóan alkalmasak sütõedények burkolására. De ne keresse a kvázikristályos tepsiket a szupermarketekben, mert tudtommal méregdrágák!
Professzor úr, ebben biztos lehet. Pedig milyen érdekes volna, hogy a könyvespolcon és a konyhában is Roger Penrose járulna hozzá szellemi és fizikai épülésünkhöz! De félre a gyarló elmélkedéssel! Ha megengedi, tovább kérdezek.
Önnek gyakran hangoztatott nézete szerint a tudatos értelem nem algoritmikus. Mit kell ezen értenünk?
Ismeretes, hogy a matematika bizonyos problémáit nem lehet számításokkal megoldani, vagyis nem készíthetõ olyan számítógépes program, amely a megoldásukat szolgáltatja. Ennek ellenére ezek jól definiált problémák. Számos ilyen van. Egyik legjobb példa erre a lefedések kérdésköre. Ha van bizonyos számú és alakú csempénk, feltehetjük a kérdést: lefedhetõ-e velük a sík, avagy nem? Robert Ferguson erre vonatkozó tétele szerint számítógéppel nem lehet eldönteni ezt a kérdést. Példa ez a nem kiszámítható problémára. A természetben is léteznek olyan folyamatok, melyek nem számíthatók, nem algoritmizálhatók. Az emberi agyvelõ mégis eljuthat a nem algoritmizálható feladatok megoldásához, mert nem biztos, hogy ilyen számítási módon közelít a kérdéshez. Ezeket a folyamatokat nagyon nehezen és csak igen finom megkülönböztetésekkel definiálhatjuk. Magának az elméletnek itt persze más tételekre is kell hivatkoznia, például fel kell használnia Gödel tételét...
Kíváncsi lennék a munkamódszerére. A sikeres gondolat megszületéséhez vezetõ út Önnél hosszabb folyamat eredménye, avagy hirtelen jönnek az eredményei?
Csaknem mindig fokozatosan jutunk el a megoldáshoz. Apró lépésekkel, kis felismerésekkel elég hosszú ideig halad az ember az úton. Ritka a villanásszerû megvilágosodás. A problémát alaposan körül kell járni, minden oldalról megvizsgálni. Jobb, ha elengedjük magunkat, nem tûzünk ki azonnal elérendõ célokat. Nem szabad nagy nyomás alatt dolgozni. A nyugodt, kényelmes állapotban jobban jönnek az ötletek. Amikor a problémán gondolkodunk, hasznos lehet, ha másoknak is beszélünk arról, esetleg szemináriumot tartunk róla. Segíthet bennünket az is, ha visszaemlékezünk olyan kérdésekre, amiket összekapcsolhatunk a vizsgált problémákkal.
Nagyon sok ragyogó ötlet születhet azáltal, hogy az ember összehoz két távolinak tetszõ dolgot, melyek összefüggése addig nem volt nyilvánvaló.
Erdõs Pállal többször volt alkalmam és szerencsém beszélgetni. Õ gyakran mondogatta, a Jóistennek van egy transzfinit könyve, amely tartalmazza a legjobb, legszebb bizonyításokat. Azután egy-egy kiválasztottnak megengedi, hogy bepillantson ebbe a könyvbe. Ekkor születnek a nagy és a szép eredmények, amelyek egyenesen a Könyvbõl valók ahogyan azt Pali bácsi mondotta volt. Penrose professzornak volt alkalma bepillantani ebbe a könyvbe? Rövidebben persze úgy is feltehettem volna a kérdést, hogy mely eredményét tartja a legjobbnak?
Elsõként, úgy gondolom, a tvisztorelméletet kell említenem. Bár még nincs befejezve, mégis vele vagyok legjobban megelégedve. Látványosabbak ugyan a csempézéssel kapcsolatos eredményeim, legtöbben talán ezt ismerik..., és ott vannak még a szingularitási tételeim. Mégis, ha sorrendet kellene felállítanom, elsõ helyre a tvisztorelméletem kerülne.
Említette az Erdõs-féle transzfinit könyvet. Nem biztos, hogy én éppen abba szeretnék belenézni. Mindenesetre fontosnak tartom a tvisztorelmélet szerkezetének feltérképezését, és annak eldöntését, vajon ráillik-e a természetre, helyes-e a matematikai szerkezet, kapcsolatba hozható-e a természet mûködésével, van-e jelentõsége annak leírásában. Ez ma még többé-kevésbé nyitott kérdés.
Paul Dirac-ot, saját bevallása szerint, kutatásaiban nagyon motiválta a szépség iránti igény. Az Ön munkásságában mekkora hajtóerõ az esztétikum?
A matematikában vagy a matematikai fizikában nagyon nehéz úgy kutatni, hogy ne hasson ránk vizsgálódásunk tárgyának esztétikája. Egyet kell értenem Dirac-kal, ez valóban fontos tényezõ, motiváló erõ. Dirac szerint az igazság mindig szép is, ebben én már nem vagyok annyira biztos. Elképzelhetõ persze, hogy ez olyan vezérelvként mûködik a matematikában, ami nélkül nehéz jelentõs haladást elérni. A lefedéssel kapcsolatos vizsgálódásaimat mindenesetre erõsen motiválta az esztétika.
A tvisztorelmélettel Ön a matematika vagy a fizika épületén dolgozik?
Az elméletnek pillanatnyilag jóval több kapcsolata van a matematikával, mint a fizikával. A fejlõdés a matematika irányában indult el, és megvallom, ez a várakozásommal és reményeimmel ellentétben történik. Dehát ugyanezt a folyamatot figyelhetjük meg a húrelmélet esetében is. A húrelméletet fizikai elméletnek fejlesztették ki, mégis, ma leginkább a matematikára gyakorol erõs hatást. Tehát mind a tvisztorelmélet, mind a húrelmélet a matematika felé fordult és egyáltalán nem világos, hogy milyen irányban keressük a fizikai elméletet.
A tvisztorelmélet még nagyon messze van attól, hogy igazi fizikai elmélet legyen. Alapvetõ gondolatok hiányoznak, nagy szakadékokat kellene áthidalnunk. A matematikai eredmények persze rendelkezésre állnak, de én nem nagyon erõltetem a matematikai irányokat, inkább az elmélet fizikai vonatkozásaival törõdöm. Ezek közül a legfontosabb az általános relativitáselmélet. A tvisztorelmélet csak akkor válik teljes értékû fizikai elméletté, ha kötelezõ módon magába tudja foglalni az általános relativitáselméletet. Ehhez azonban még nagyon hosszú utat kell megtennünk.
Egy bölcs fizikus professzor barátom nemrégiben azt mondta nekem, hogy a fizikai kutatások kertjében manapság a matematika virágai pompáznak. A fizikai intuíció ma egyre inkább a matematikától származik, nem a kísérletektõl. Mi errõl a véleménye?
Pontos a diagnózisa. Manapság az alapkutatásokat mindenképpen a matematika inspirálja, a fizikai kísérletek kevéssé ösztönöznek. Sajnos ez az igazság. Engem is a matematika inspirál kutatásaimban.
Sokkal szorosabb és gyakoribb kapcsolatra lenne szükségünk a kísérletekkel, a világgal. Addig, amíg ezt a kapcsolatot nem találjuk meg, nem lehetünk biztosak abban, hogy mit kell komolyan vennünk. Einstein, aki nagyon sok mindent tett a tudományban, többek között megalkotta az általános relativitáselméletet, nem nagyon támaszkodott a matematikára. Esetében éppen fordított volt a helyzet: hihetetlenül erõs fizikai intuíciója volt, remek fizikai ötletei, ezek megvalósításához azonban matematikát kellett tanulnia. Neki az elméletéhez volt szüksége a matematikára.
Miután elméletét sikerre vitte, felismerte, hogy a matematika milyen hatalmas eszköz és milyen további lehetõségeket, távlatokat nyújt. Ezért késõbbi munkájában, amikor az általános térelméletet igyekezett kidolgozni amire sokan azt mondták, csak vesztegeti vele az idejét , már jelentõs mértékben matematikai meggondolások ösztönözték. A korábbi eredményeihez mérten ekkor már nem tudott hozzájárulni a tudományhoz. Ez azonban csupán azt bizonyítja, hogy Einstein a matematikában nem volt elég erõs. Ugyanakkor elõfordul az is, hogy matematikusoknak, akiknek a matematikai intuíciójuk az erõsebb, sikerül jelentõs hatást gyakorolniuk a fizikára. Vegyük példaként a mértékelméleteket és a kvantumelméletet, melyek ma a részecskefizika elméleti alapját képezik. Úgy gondolom, helyes, hogy mostanában a kutatások matematikai oldalát erõltetik. Mindez persze nem újdonság, már Maxwell elméletének megszületésekor is a matematika volt az ösztönzõ erõ.
Összegzésként igazat kell adnom a kérdésében megfogalmazott meglátásnak: az elméleti fizikai kutatások túlságosan elmentek a matematika irányába.
A matematikának mely területei lettek hangsúlyosak napjaink vezetõ fizikai kutatásaiban?
Nagyon divatos lett a kvantumcsoportok elmélete, sokan dolgoznak a húrelméletekkel, számos új eredmény látott napvilágot az algebrai geometriában, mégsem világos, hogy mindez igazából fizikának számít-e, hasznot húz-e ebbõl a fizika.
A fizikai gondolkozás ugyanakkor számtalan matematikai kutatást indított meg. Visszafelé mindez nem mûködik hasonló hatásfokkal. Az új matematikai eredmények nemigen vezetnek igazi fizikai megértéshez, elõrelépéshez a fizikában. Az új fizikai modellek mindenesetre rendkívül bonyolult matematikai eszközöket követelnek.
Pedig az elméleteknek illene mindinkább egyszerûsödniük...
Igen, ez így van, mégis az figyelhetõ meg, hogy végül is mindig ugyanaz a formalizmus tûnik elõ, újabb és újabb köntösben. A kvantumtér-elmélet, a topologikus térelmélet nem sok jót hoz a fizikának, ezt bizton állíthatom.
Szeretném rávenni egy kis jóslásra. Véleménye szerint az elkövetkezõ tíz évben milyen figyelemre méltó eredmények várhatók a matematika Ön által belátott területein?
Kockázatos jóslásokba bocsátkozni. Mégis, határozott meggyõzõdésem, hogy a kvantumelméletben forradalmi változásnak kell bekövetkeznie. Annál is inkább, mert a kvantumelméletnek e pillanatban így nincs értelme. A kvantummechanika igen jól mûködik nagyon kis rendszerek, atomok, molekulák világában. Nagyobb szerkezetek esetében is jól alkalmazható, például a szupravezetõk leírásakor kis energiakülönbségek esetén. Két eljárás van: egyik a Schrödinger-egyenlet, a másik a mérés. Határozottan ki merem jelenteni, hogy ez a kétfajta eljárás két szélsõ esetben nem kompatibilis egymással. Véleményem szerint, ami a kvantumelméletet illeti, a fizikai megértésünkben mélyreható változásoknak kell bekövetkeznie. Sok fizikus egyetért velem ebben, Budapesten is van egy iskola beleértve Károlyházy Frigyes professzort , akik hasonlóképpen gondolkoznak.
Mindenesetre ennek a forradalomnak egyelõre nem látom a formáját. De lesz ilyen változás, biztosan eljön. Lehet, hogy a jövõ évben, lehet, hogy csak 200 év múlva...
Tudom, nem egészen sportszerû olyant kérdezni, melynek megválaszolásához több nap sem elegendõ, nemhogy egy néhány órás beszélgetés. Mégis érdekelne a válasza: Mire való, mire jó a matematika?
Tetszik a felvezetés! A probléma itt az, mit jelent, hogy jó valamire. Jó-e akkor, ha valakinek örömet szerez, élvezetet nyújt? Jó-e nekünk például egy szép, klasszikus zenemû? Az örömforrás említése önmagában még gyenge érv a matematika védelmében. A matematika azon kívül, hogy nagyon sok embernek szerez örömet, egész sor tudományterületet is alátámaszt. A tudomány a matematikán alapul, alapvetõen függ a matematikától. Megkérdezheti, persze, hogy jó-e a tudomány valamire?
Isten õrizzen! Ilyeneket nem kérdezek.
Jól teszi, ennek megválaszolása ugyanis túl messzire vezetne. A matematikusok nem azért mûvelik a matematikát, hogy az jó legyen valamire. Ebbõl a szempontból a matematikusok eredményei tulajdonképpen melléktermékek. A matematikának önmagában is ösztönzõ szerepe van. Óriási a hatása a tudományokra, de nagyon kis része gyakorolja ezt a hatást. A matematika legnagyobb részének igazán csak azokra van hatása, akik foglalkoznak vele.
Furcsa ez a kérdés, mert bizonyos szempontból nyilvánvaló a rá adható válasz. A matematikának parányi része hajt közvetlen hasznot, a matematika túlnyomó többségét saját kedvtelésükért ûzik az emberek.
Nézze el nekem, hogy nemcsak a matematikára, hanem a matematikát mûvelõ emberre is kíváncsi vagyok. Érdekel, mik az Ön legfõbb tulajdonságai, melyek az életben segítették?
Nehéz erre szenvedélymentesen válaszolni. Nem lehet csak úgy hátradõlni a székben, mindentõl elvonatkoztatni és kívülrõl szemlélni önmagunkat.
Jó, akkor kissé általánosítom a kérdést. A matematika sikeres mûveléséhez mi szükségeltetik, mik a siker feltételei a matematikában?
Érdeklõdni kell a téma iránt, izgalmasnak találni a problémákat. Másként nem megy. Ahhoz, hogy az ember sikeres legyen, szeretnie kell a matematikát. Kezdetben hasznos, ha hibátlanul tudunk számításokat végezni. Késõbbiekben ez elhalványul, sokkalta fontosabb lesz, hogy felismerjük és értékeljük a téma szépségét. Megtaláljuk benne azt, ami önmagában is vonzó és értékes. Nem tudom, mindez megtanulható-e, de ha elég hosszú ideig foglalkozunk valamivel, akkor hamarabb felismerjük rejtett kincseit.
Kik voltak azok az emberek, akik erõsen hatottak az Ön gondolkodására, akik formálták tehetségét?
Legnagyobb hatással apám volt rám, és a családból még Oliver testvérem. Odahaza apám olyan atmoszférát teremtett, mely a matematikát mindannyiunk számára izgalmas szellemi kalanddá tette. Ez volt nálunk az érdeklõdés középpontjában, nem a futball vagy a krikett. Ha nem így lett volna, most valószínûleg nem lennék itt.
Késõbb Cambridge-ben Dirac és Bondi elõadásai fogtak meg leginkább. Dirac elõadásai a kvantummechanikáról, Bondié az általános relativitáselméletrõl szóltak. Sokat jelentett nekem Dennis Bondi barátsága, aki mindig naprakész volt a relativitáselmélet és a kozmológia fejleményeiben. Több olyan izgalmas dologról tudott, ami akkoriban lázban tartotta az embereket, és engem is rabul ejtett.
Már több mint tíz éve annak, hogy Jakov B. Szinaj professzorral folytatott beszélgetés végén feltettem a sablonos kérdést: mivel tölti az idejét, amikor éppen nem matematikával foglalkozik. Rövid gondolkodás után ezt válaszolta: sorban állok Moszkvában az élelmiszerüzletek elõtt. Azután, átérezve, hogy ezt így nemigen közölhetjük le, módosított: tudja mit, írja inkább azt, hogy segítek a feleségemnek a háztartásban. Úgy is lett, de ebbõl váratlan bonyodalom támadt. A feleség elolvasta az interjú kéziratát, és kérdõre vonta Szinajt az állítás valóságtartalmát illetõen. Ismét módosítanunk kellett a választ, hogy a feleség igazságérzetét se bántsuk meg.
Úgyhogy, a hosszú elõkészítés után rövid a kérdésem: mi az Ön hobbija?
Jó a történet. Én, ha szabad idõm van, igyekszem könyvet írni. Ezen kívül pihenésképpen mindenféle ostoba dolgot csinálok, például tévét nézek...
A munkahelyén dolgozik, vagy odahaza?
Az irodámban nagyon ritkán nyílik lehetõség matematikai kutatásra. Mindig mással kell foglalkozni. Adminisztrálok, leveleket és jelentéseket írok, meg ajánlásokat diákjaimnak. Azután jönnek például a rádiótól és mindenáron azt akarják, hogy fejtsem ki a mesterséges intelligencia lényegét. De öt perc alatt! Annyi idejük van rá. Így lehetetlen kutatni, ha percenként benyit az emberhez valaki.
Akkor mikor dolgozik? Mikor tud magára maradni a matematikával?
Amikor egyik helyrõl a másikra gyalogolok. Reggel borotválkozás közben, vagy amikor éppen felszállok a buszra.
Nagyon nehéz elérni, hogy szabadidõnk maradjon a matematikára. Ahhoz, hogy az ember kutatni tudjon, fiatalnak kell lennie. Minél öregebbek leszünk, annál kevesebb idõnk marad a kutatásra.
Professzor úr, az elsõ kérdésemmel kapcsolatos problémakör nem hagy nyugodni. Elképzelhetõnek tartja, hogy a világ legjobb matematikusa egykor egy komputer lesz?
Nem, azt egyszerûen elképzelni sem tudom. A számítógépek nem képesek erre. De sakkozni tudnak, ez kétségtelen.
Ha mégis..., ne adj Isten, mégis bekövetkezik ez, akkor hol találom meg Önt? Hol beszélgethetünk el újra egy kicsit a mesterséges intelligenciáról?
Oxfordban megtalálhat, ha nem leszek éppen Budapesten.
Az interjút készítette:
STAAR GYULA
| Természet Világa, | 128. évf. 12. sz. 1997. december, 534-538. o. |
| https://www.kfki.hu/chemonet/TermVil/ | |
| https://www.ch.bme.hu/chemonet/TermVil/ |