SIMONYI KÁROLY
A fizikai alapkutatások frontvonala a harmadik évezred küszöbén
Összegzés és kitekintés*

---

A fizikai kutatások frontvonala a harmadik évezred küszöbén (1990-ben) különleges helyzetben van. Szigorúan véve a fizikatörténet, vagy általánosabban az emberi történelem bármely korszaka egyszeri, megismételhetetlen és így valamiképpen különleges, de egyes esetekben a számunkra releváns sajátosság tettenérhető, jól megfogalmazható. Ez különösen akkor tűnik elő, ha egy másik analóg helyzettel vetjük össze. Ilyen összehasonlítási alapként a századforduló fizikája kínálkozik.

 A jelen helyzet fő jellemvonásait az alábbiakban foglalhatnánk össze.

 1. Létezik egy elmélet, a standard elmélet, vagy standard modell. Ellentmondásmentes, nagy belső koherenciával rendelkezik és prediktiv, jós erejét is bebizonyította.

 A standard elmélet a négy alapvető kölcsönhatásból, az elektromágneses, a gyenge, az erős és a gravitációs kölcsönhatásból az első kettőt – az elektromágneses és a gyenge kölcsönhatást – egyetlen kölcsönhatássá, az elektrogyenge kölcsönhatássá olvasztja össze (Glashow, Salam, Weinberg, 1967/68), míg a független, különálló, erős kölcsönhatás leírására a kvantumchromodinamika (QCD), vagy színdinamika szolgál (Gell-Mann, Fritsch és Leutwyler, 1973). A gravitációs kölcsönhatásról a standard elmélet nem tud újat mondani.
 Az elmélet leglátványosabb sikere az elektrogyenge kölcsönhatást közvetítő részecskéknek, a W⁺, W^-, Z⁰ vektor-bozonok létének
és tömegének megjóslása, majd kísérleti igazolása (Rubbia-vezette kutatócsoport, CERN, 1983).

 2. Úgy tűnik, hogy az az út, amely pusztán szimmetria megfontolásokkal a kvantumelektrodinamikából (QED) az elektrogyenge kölcsönhatáshoz, ill. a színdinamikához, a kvantumchromodinamikához (QCD) vezetett, tovább követhető a nagy egységesítés elméletéig (GUT = Great Unification Theory), de talán még ezen is túl a mind a négy kölcsönhatást, és ezzel a minden jelenséget egybefoglaló elméletig (TOE = Theory of Everything): így újból felsejlik a fizikai alapkutatások befejezésének egyesek számára kívánatos, mások számára visszariasztó víziója.

 3. A makrokozmosz problémája, vagyis az Univerzum keletkezésének és fejlődésének problémája és az elemi részecske-fizika problémája azonossá válik és csak együtt oldható meg. A kulcsprobléma a gravitációs kölcsönhatás elméletének beépítése a kölcsönhatások egységes elméletébe.

 4. A születendő, kidolgozás alatt álló elméletek kísérleti igazolása csak olyan nagy részecske energiáknál lehetséges, amelyek megvalósítása földi laboratóriumokban a jelenlegi technikai és financiális lehetőségeket messze meghaladja. Ezzel lehetetlenné válik az elmélet és kísérlet eredményes összjátéka, a helyes törvényszerűségek keresésének eddig jól bevált sémája: elmélet ® kísérlet ® elmélet ® kísérlet...

 5. De még a közvetett kísérleti bizonyítékok keresése is olyan technikai és ennek megfelelő financiális eszközöket igényel, amelyek még egy gazdag ország költségvetése számára is súlyos terhet jelentenek. Ezzel az a  paradox helyzet állt elő, hogy minél távolabb esik egy fizikai kutatás a mindennapi élet problematikájától, minél inkább csak az  elefántcsont-tornyukba   visszavonul  elméleti fizikusokat érdekli, annál nagyobb szüksége van az élet durva realitását reprezentáló pénzügyi támogatásra.

6. Az ősrobbanás, a világegyetem keletkezése felveti a fizikai törvények létkategóriájának inkább filozófiai, mint fizikai problémáját (1. idézet).

 A továbbiakban az itt elmondottakhoz fűzünk néhány kiegészítő megjegyzést, elsősorban a vezető fizikusok véleményére támaszkodva.

 Először is az 1. ponthoz csatlakozva részletezzük kissé a standard elmélet eredményeit.

 A fundamentális részecskék két nagy csoportba oszthatók (1. ábra): a feles spinű részek, a fermionok tekinthetők az anyag tulajdonképpeni építőköveinek, míg az egész spinű részecskék feladata az ezek közötti erőhatás közvetítése.

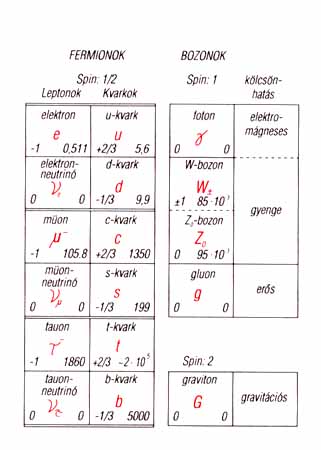
1. ábra.  Ezeket tekintjük fundamentális részecskéknek 1990 táján. A feles spinű részek, a fermionok, az anyag tulajdonképpeni építőkövei, míg az egész spinű részek, a bozonok, a közöttük működő erőhatások közvetítői. A három fermion-családot kettős vonallal határoltuk el egymástól. 17 részecskét ábrázoltunk. Figyelembe kell azonban vennünk, hogy mindegyik kvarkféleség három színben fordul elő, vagyis három féle „színtöltéssel” van ellátva; azon kívül még 8 féle gluon is létezik. Ha a felsorolt részecskékhez még az antirészecskéket is hozzászámítjuk, a fundamentális részecskék száma ismét 50 fölé emelkedik.
 Az ábrán mindenegyes részecskének megadtuk a nevét, a jelét, a töltését (az elemi töltés hányadában) és a (néhol csak a hozzávetőleges, becsült) tömegét MeV-ban. A kvarkok betűjelét a felfedezők által adott megnevezés első betűje adja. Ezek rendre  u: up (fel); d: down (le); c: charmed (bájos); s: strange (különös, ritka); t: top vagy truth (tető, vagy igazság); b: bottom, vagy beauty (fenék, vagy szépség)
 

 A fermionok három jól elkülöníthető családba rendeződnek: mindegyik család két nehéz részecskéből – ezek a kvarkok – és két könnyű részecskéből (leptonból) áll – egy-egy, az elektronhoz hasonló töltött részből és egy-egy neutrínóból.

 Az erős kölcsönhatás szempontjából a leglényegesebb az a tény, hogy a kvarkok mindegyike színes, pontosabban kifejezve színtöltéssel van ellátva – ez háromféle lehet – amely színtöltésnek a kvarkok közötti erős kölcsönhatás létrejötte szempontjából ugyanolyan szerepe van, mint az elektromos töltésnek az elektromágneses kölcsönhatás létrejöttében: ezek a forrásai (létrehozói) a kölcsönhatást közvetítő részecskéknek, a gluonoknak.
 A hadronokban (protonokban, neutronokban, mezonokban) ezen, a gluonok által közvetített „színerők” tartják össze a kvarkokat (2. ábra). A hadronok maguk „színtelenek”, tehát a színtöltésük nulla. A protonokban és   neutronokban a   három különböző szín alkalmas szuperpozíciója, a mezonokban a szín-antiszíné gondoskodik erről a színsemlegességről.

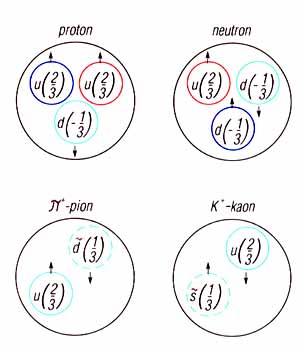
2. ábra. Néhány hadron kvarkszerkezete: a proton és neutron (két nukleon), a p+-pion és a K+-kaon (két mezon). A színtulajdonság jelzésére az elterjedt gyakorlatnak megfelelően a vörös, kék, zöld színt, míg az antirészecskék színeinek (antivörös, antikék, antizöld) jelzésére az eredeti szín szaggatott változatát használtuk. Az ábráról az alábbiak olvashatók le:
1) A kvarkok együttes töltése megadja a részecske (mérhető) töltését.
2) A két nukleon számára kiadódik az 1/2 (feles) eredő spin. A két mezon, a kísérleteknek megfelelően nulla spinnel rendelkezik.
3) A „ritkaság” (strangeness) az s-kvark jelenlétével függ össze.
4) Az eredő színtelenség (a színerők szempontjából „fehér”) állapot a három szín együttes fellépéséből (a nukleonoknál), vagy a szín-antiszín kombinációból adódik (a mezonoknál).
 

 De éppen úgy, ahogy az elektromosan semleges molekulák egymáshoz az elektromos szórt-téren (Restkraft, Van der Waals-erő) keresztül kapcsolódnak, a színsemleges protonok és neutronok a maradék, szórt színerő segítségével kötődnek. Ez az, amit magerőnek hívunk és erről kell kimutatni, hogy egyenrangú a p-mezon közvetítésű leírással.

 Szabad állapotban eddig még nem figyeltek meg kvarkot. Úgy tűnik, hogy a kvarkok csak mintegy zsákba bezárva létezhetnek, mégpedig színsemleges struktúrában. A legújabb elméleti vizsgálatok szerint viszont elképzelhető, hogy a kvark-hadron fázisátalakulás viszonylag kis energiasűrűségű maganyagban is végbemehet. Az ilyen irányú kísérleti vizsgálatok megindultak, de eredmény csak a 21. század első évtizedeiben  várható.

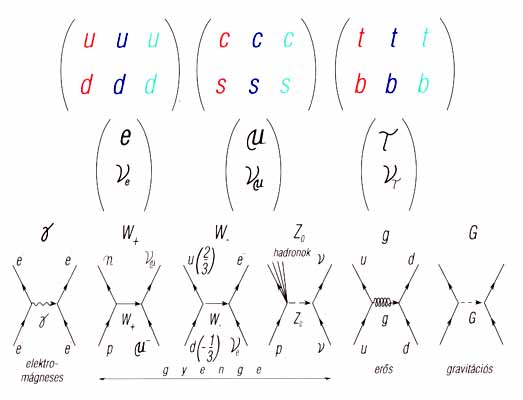
3. ábra. A fundamentális részecskék egy másik elrendezése, amelyben a kvark-lepton szimmetria jobban kitűnik. Mint annak idején a periódusos rendszerben, itt is a még üres helyek mutattak rá az új részecskék létezésére. A Feynman-diagramok segítségével ábrázoltuk a közvetítő részek szerepét az egyes kölcsönhatásoknál. A gyenge kölcsönhatásnál az első a müon-befogást, a második a neutronbomlást ábrázolja (n ® p + e^–  + _e). Összehasonlítva ezt a proton és neutron 2. ábrán látható kvarkszerkezetével, látjuk, hogy a neutronbomlás a kvarkok szintjén egy d-kvark u-kvarkká való átalakulásából áll. Végül az utolsóban a gyenge kölcsönhatás közvetítő részecskéje a semleges Z⁰ bozon: nagy energiájú neutrínó rajta keresztül lép egy protonnal kölcsönhatásba, a neutrínó elveszíti energiájának nagy részét, amely hadronok sokaságának energiájaként jelentkezik.
 Az erős kölcsönhatást a két (színtöltéssel ellátott) kvark között a gluon hasonlóképpen közvetíti, mint a foton (az elektromos töltéssel ellátott részecskék között) az elektromágneses kölcsönhatást.
 A gravitációs hatás közvetítő részecskéjéről ez idő szerint semmit sem tudunk.
 

 A 3. ábrán kissé más elrendezésben újra lerajzoltuk a fundamentális részecskéket, hogy egyrészt a kvark–lepton szimmetria jobban érvényesüljön – ennek ugyanis nagy heurisztikus jelentősége volt a standard elmélet kialakításában, – másrészt hogy a közvetítő részecskék szerepét a Feynman-diagramok segítségével képiessé tegyük. Így újraértelmezhetők az ismert jelenségek, mint amilyen például a neutron bomlása: ez végső soron egy d-kvark u-kvarkká való átalakulásából áll. Ugyanakkor sokkolóan igaznak találjuk Glashow megállapítását. Szerinte a lét alapaktusa (The Fundamental Act of Becoming), amelyből minden jelenség összetevődik: egy részecske (kvark, elektron, neutrino) emittál (vagy abszorbeál) egy másik részecskét (gluont, fotont, vektorbozont), vagyis a közvetítő részecskét (4. ábra).

4. ábra. A lét alap aktusa (The Fundamental Act of Becoming) Glashow szerint az elképzelhető legegyszerűbb jelenség: egy részecske kibocsát (vagy abszorbeál) egy másik részecskét. Egy a természetben végbemenő „elemi” jelenség is már több ilyen alapaktusból áll: a semleges kaon K⁰®p + e^– + n_e bomlása az ábráról leolvashatóan hat alaptörténés eredménye.
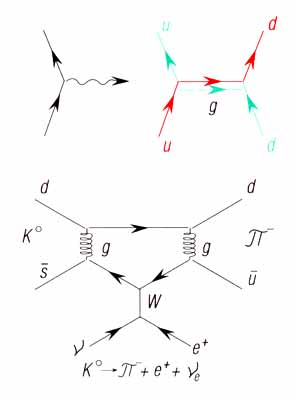
 A kvarkok közötti erőhatás csak első megközelítésben hasonlít az elektromágneses erőhatásra. A gluonok ugyanis maguk is „színesek”, vagyis színtöltést hordoznak. Ennek megfelelően egymással is (erős) kölcsönhatásba tudnak lépni. Ez a viszonyokat bonyolulttá teszi; ezzel kapcsolatos az a tény is, hogy a kvarkok közötti erőhatás a hadronok belsejében kis távolságoknál lecsökken: a kvarkok aszimptotikusan szabadok.
 A nyolc gluon mindegyike kétféle színtöltést hordoz: egy-egy színt, a három szín egyikének antiszínével kombinálva. (A lehetséges 9 kombináció közül az elmélet csak nyolc realizálását engedélyezi.)
 Az ábra egy vörös u-kvarkot mutat, amely egy vörös-antizöld töltéssel ellátott gluont bocsát ki, ezzel önmaga zöld u-kvarkká, partnere zöld d-kvarkból piros d-kvarkká változik.
 

 Anyagi világunk felépítéséről így egy viszonylag egyszerű  és áttekinthető képet kapunk (5. ábra).

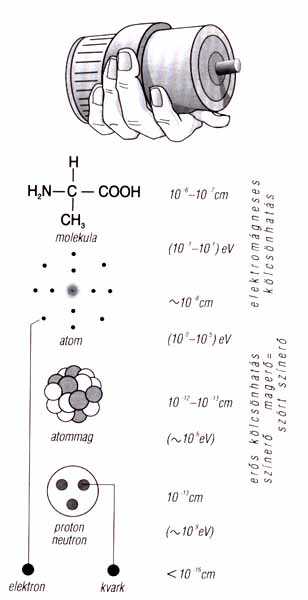
5. ábra. A bennünket körülvevő, érzékeinkkel közvetlenül megtapasztalható makrovilág felépítése – legyen az élettelen vagy élő, művi vagy természetes – viszonylag egyszerű. Első fokozatban a kémia molekulákra bontja az anyagot, mint elemi építőkövekre. A molekulák atomokból állnak – néha több ezerből, vagy több százezerből – és így méretük szinte „makroszkopikus”. Az atomokat végső soron a foton közvetítette elektromágneses kölcsönhatás kapcsolja molekulává. Ez az elektromágneses kölcsönhatás szemléletesen jelentkezik a pozitív töltésű atommagok és a negatív töltésű elektronok atommá kötődésénél. A magok stabilitását a protonok és neutronok között működő magerők – maradék (szórt) színerők – biztosítják. Végül egy-egy protont vagy neutront u- és d-kvarkokból a gluonok közvetítette színerők ragasztják össze.
 Így saját testünk is végső fokon u- és d-kvarkokból áll. Egy átlagos emberi test 7·10²⁸ u-kvarkból, 6,5·10²⁸ d-kvarkból és 2,5·10²⁸ elektronból áll [2].
 A méret mellé odaírtuk azt az elektronvoltokban kifejezett energiát, amely az adott rendszer állapotának megváltoztatásához szükséges.
 A „makroszkopikus test” itt egy kéz, amely az ember fizikai teljesítményével azonos   teljesítményű – 70 wattos – motort tart.
 

 Vizsgáljuk meg összehasonlításként a századforduló fizikájának helyzetét: ott a kérdőjelek mellett szikrázó ellentmondásokat is találunk; a klasszikus fizika sok jelenségre nem tudott válaszolni, néhány határozott, kategorikus válasza viszont rossz volt. A standard elmélet is tele van kérdőjellel, alkalmazása azonban nem vezet sehol ellentmondáshoz.

 De van egy súlyos fogyatékossága: a standard elmélet feltételezi a Higgs-bozonok létét. Ezek a bozonok a Higgs-tér közvetítői és fontos szerepet játszanak: ők felelősek a gyenge kölcsönhatást közvetítő W⁺, W^-, Z⁰ vektorbozonok tömegéért. Viszont a Higgs-bozonok létét eddig nem sikerült kimutatni.

 Belső koherencia, ellentmondásmentesség, jóserő: mindezek a jó tulajdonságok nem tudják feledtetni azt a tényt, hogy az elmélet egy sor lényeges kérdésre nem tud válaszolni.

 Glashow 12 kérdést sorol fel. Ezek közül néhány:
 Miért van éppen három fermion család? Miért olyan hasonlatosak ezek?
 Miért egyezik meg pontosan a proton és az elektron elektromos töltése?
 Van a fotonoknak és a neutrínóknak véges nyugalmi tömege?
 Létezik mágneses monopólus?
 Mekkora a proton élettartama? Végtelen? És így valóban stabilnak tekinthető?

 Glashownak és Georginak sikerült néhány kérdésre a választ sugalmazni. Ők a 2. pont alatt jelzett utat követték 1974 óta és megteremtették a  Nagy Egységesítés, vagy a Nagy Egyesítés (GUT= Great Unification Theory) elméletét.

 Ismerkedjünk meg kissé részletesebben a 2. pontban vázolt úttal és a szereplő szimmetriákkal.

 A negyvenes évek elején a kvantumelektrodinamika azzal érte el átütő sikerét, a hihetetlen számszerű pontosságot, hogy sikerült az elektromos kölcsönhatás kiszámításánál fellépő, többszörösen végtelen értékek hatását kiküszöbölni. Ezt a renormalizálásnak nevezett eljárással érte el. A renormalizálhatóságot viszont az a tény tette lehetővé, hogy az elektromágneses tér mértékszimmetrikus, mérték-invariáns (Eichsimmetry, Eichinvarianz, Gauge-Simmetry). Kis túlzással azt is mondhatjuk, hogy ahogy az optika a legrövidebb idő elvéből következik, úgy következik az egész elektrodinamika, beleértve még a foton létét is a maga összes tulajdonságaival – nulla nyugalmi tömeg, egészszámú spin – a mértékszimmetriából. Ez az egyszerű, szépségében is eredményes minta nagy csábítást jelentett az általánosítás megkísérlésére.

 A mértékszimmetria az általános szimmetria csoport speciális esete. Akkor mondjuk, hogy egy fizikai elmélet mértékszimmetriával rendelkezik, ha az egy mértéktranszformációval szemben invariáns, vagyis mérték-invariáns. Maga a mértéktranszformáció viszont annyit jelent, hogy az elméletben szereplő térjellemzőkhöz meghatározott tér-idő függvényeket kapcsolunk, vagy megfelelő fázistényezővel megszorozzuk; ha mármost eközben a fizikailag releváns (méréssel nyerhető) értékek nem változnak, az elmélet mértékinvariáns, vagy mértékszimmetrikus. A legegyszerűbb példa: az elektromos erőhatás nem változik, ha a potenciál értékéhez tetszés szerinti (konstans) értéket adunk. Vagy kissé általánosabban: a Maxwell-egyenletek invariánsak a négyespotenciál mértéktranszformációjával szemben.

 A mértékszimmetriák leírására mint matematikai diszciplína a csoportelmélet szolgál. A problémák kezelésére viszont a csoportok mátrix reprezentációja a legalkalmasabb. Az itt szereplő speciális csoportok az unitércsoportok alcsoportjai. (A szokásos SU(n) jelölésnél az S betű a speciális, az U az unitér szóra utal, n pedig a csoport rangja.) Az unitér csoportok olyan mátrixok –  az unitér mátrixok – segítségével reprezentálhatók, amelyekre  érvényes az ^T = A^-1 összefüggés, ahol  azon mátrix, amely az  A mátrixból úgy áll elő, hogy mindegyik eleme helyett annak konjugált komplex értékét írjuk. A^T pedig az A transzponáltja, amelynek tehát sorai és oszlopai fel vannak cserélve, A^-1 pedig az A mátrix inverze.

 A speciális SU(n) unitér mátrixok determinánsának értéke +1.

 Az elektromágneses tér mértékszimmetriáját az U(1) szimmetriamátrix írja le. A közönséges térben ez a lehető legegyszerűbb szimmetriát, a kör forgásszimmetriáját jelenti. Mint ahogy említettük, ez a szimmetria teszi lehetővé a renormalizálást és ezen keresztül az elektron anormális mágnes momentumának és a Lamb-eltolódásnak hihetetlenül pontos (elméleti) meghatározását.

 Az elektrogyenge kölcsönhatás alapjául az SU(2) x U(1) kombináció szolgál, (ahol x a szimmetriacsoportok direkt szorzatát jelöli). Az erős kölcsönhatás elméletének, a kvantumszindinamikának hátterében az SU(3) szimmetria áll. A standard elmélet mértékszimmetriája tehát az SU(3) x SU(2) x U(1) kombinációjának vehető. Mármost Glashow és Georgi egyetlen csoportot kerestek, amely a három kölcsönhatás  egységes elméletének bázisául szolgálhatna. Az SU(5) csoportot alkalmasnak találták erre a célra.

 Így állt elő a Nagy Egységesítés Elmélete.  Ez az elmélet feleletet adott néhány eddig megválaszolatlan kérdésre. Megadja a kvarkok és az elektronok töltéseinek értékét, a fotonok számára pedig a nulla nyugalmi tömeget írja elő. Megmagyarázza a kozmosz „felfúvódását”.

 És egy új, nagyon fontos következmény: lehetséges az átmenet a két fermion-család, és így a leptonok és a hadronok között. Ez pedig annyit jelent, hogy a proton instabil! Az elmélet megadja az élettartamot is: 10³⁰ év. A felezési idő, a 10³⁰ év 20 nagyságrenddel nagyobb, mint az univerzum életkora. De ha meggondoljuk, hogy 1 kg anyag nagyságrendben 10²⁷ nukleont tartalmaz, úgy az adódik ki, hogy 1 tonna anyagban 1 nukleon/év bomlás várható, így 1000 tonna anyagban 2-3 bomlás megy végbe naponta. Ennek kimutatása szinte irreális technikai és financiális nehézséget jelent, ennek ellenére a kísérletek – mindeddig eredmény nélkül – már folynak.

 Az elmélet közvetlen bizonyítéka természetesen az lenne, ha sikerülne az ezen egységes kölcsönhatás közvetítő részecskéit, az X-bozonokat megfigyelni ugyanúgy, mint ahogy az elektrogyenge kölcsönhatás „experimentum crucis”-a a W⁺, W^-, Z⁰ bozonok észlelése volt. Minthogy azonban ezen X-bozonok tömege 10¹⁵ GeV nagyságrendben  van,  –  szemben  az  előbb  említett  részecskék  100 GeV nagyságrendjével, ez a közvetlen kísérleti bizonyíték messze túl van jelenlegi technikai lehetőségeinken.

 Az elméleti fizikusok – érthetően mit sem törődve a közvetlen kísérleti igazolás szinte elvi lehetetlenségével – tovább haladnak az eddig bevált úton. Az egyik ilyen elmélet, a Susy (szuperszimmetria) bázisa az  SU(8)  szimmetria  csoport. Ez az  elmélet  nemcsak a két fermion család közötti átmenetet engedi meg, mint ahogy ezt a GUT teszi, hanem elmossa a bozonok

és a fermionok közötti határt: nem tesz különbséget tulajdonképpeni elemi részecskék és közvetítő részecskék között. Ezek mind egyetlen szupercsalád tagjai. Ezen elmélethez tartozó karakterisztikus tömeg, ill. energia a Planck-tömeg: 10¹⁹ GeV.

 Egy másik, nagyon divatos elmélet a Superstring (szupersztring, szuperhúr) elmélet (TOE = Theory of Everything). Ennek csírái igen korán, már a hatvanas évek elején megtalálhatók Gabrielle Veneziano műveiben. Ő azonban tisztán az erős kölcsönhatás keretei között konstruált hasonló szerkezeteket. John Schwarz és Michail Green ehhez kapcsolódó munkáira csak a nyolcvanas évek második felében figyeltek fel. Az elmélet a súlypontot a tér topológiájára helyezi át: világunk valójában 9 dimenziós, de ebből hatot  nem észlelhetünk   közvetlenül,    mert ezek   egy  Planck-hossz (10^-33 cm) méretű sokdimenziós hengerre vannak valamiképpen „felcsévélve”. Az elmélet egyik legeredetibb és legjellemzőbb – névadó – vonása: a részecskék nem pontszerű struktúrák, hanem inkább húr, vagy hurok alakúak. Ezen húroknak a kilencdimenziós térben felvett különböző vibrációs formái határozzák meg a részecskék jellegét, mármint, hogy fotonként vagy kvarkként észleljük őket.

 Mennyire lehet komolyan venni a szuperhúr elméletet? Érdemes-e időt, tehetséget, pénzt áldozni rá?

 Glashow kategorikus és szarkasztikus nemmel válaszol (2. idézet). Feynman megjegyezte, ő tudja jól, hogy a  bölcs öregek az új dolgokat gyakran ostobaságnak tartják és ezzel mind a jelen fiataljai, mind az utókor előtt nevetségessé válnak; ennek ellenére a szuperhúr elméletet ostobaságnak tartja.

 Idézzük azonban az elmélet kezdeményezőinek és legaktívabb harcosainak, Schwarznak és Greennek optimista kicsengésű jóslatát [5].

 Nem kétséges, hogy a szuperhúr elmélet nagyon impresszív. Az elméleti fizikusok meggyőzően beszélnek az elmélet hihetetlen szépségéről és gazdagságáról... Ha az elmélet valóban az összes részecskék és erők kvantitatív magyarázatával tud szolgálni, úgy ez az elmélet az emberi történelem legnagyobb tudományos győzelmének tekinthető. Nem csoda tehát, hogy számos kutató régóta művelt területét máról holnapra otthagyta, hogy a sztringfizikusokhoz csatlakozzék. Manapság alig van a részecskefizikával vagy a gravitációval foglalkozó szeminárium, folyóirat, ahol a sztring-elmélet ne kerülne szóba.

 Tegyük fel, hogy sikerül az alapvető elveket megértenünk és az alapegyenletek egyértelmű megoldását megtalálnunk. Ezen megoldás birtokában lehetővé válik a hatdimenziós tér topológiai tulajdonságainak részletes feltárása. Az eredményekből arra is következtethetünk, hogy hány és milyen sajátosságú részecskék léteznek az alacsonyabb energiarégiókban; tömegeik arányát éppúgy megkaphatnánk, mint az egymásra hatás intenzitásának viszonyait. De éppen az ilyenfajta információk azok, amelyek a (földi) laboratóriumban elvégzett kísérletek eredményeivel összevethetők.

 A közvetlen kísérletezésről természetesen szó sem lehet; felvetődik a kérdés, léteznek-e olyan valós viszonyok, ahol az elmélet követelte törvényszerűségek szerint folynak le a jelenségek. Igen, a Planck-érában  az  Ősrobbanás  utáni 0-10^-43 s  intervallumban (6. ábra).

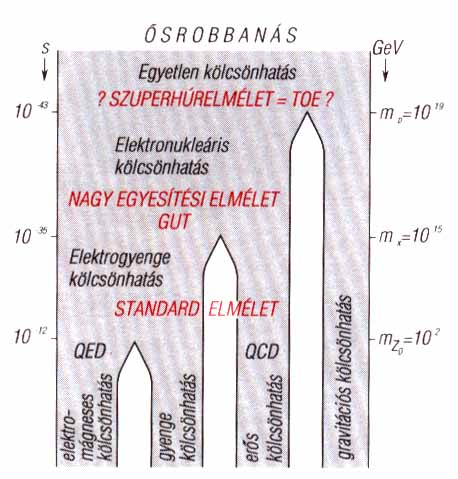
6. ábra. A fundamentális részecskék fizikájának legizgalmasabb jelenségei a Planck-érában, a 0–10^-43 s intervallumban játszódnak le. Itt mind a négy kölcsönhatás egyetlenegy kölcsönhatásba olvad össze. Ezen kölcsönhatás törvényszerűségének ismerete azt jelentené, hogy ismerjük a fokozatosan szétváló kölcsönhatások tulajdonságait is. Vagyis meg tudnánk magyarázni a mindennapi valóság történéseit.
 Például azt is, hogy a 10_-12 s táján már teljesen szétvált kölcsönhatások intenzitásának aránya miért éppen a következő:
erős: elektromágneses: gyenge: gravitációs = 1:1/137:10^-5:10^-39.
 Létünket a világban éppen ez a viszony határozza meg. Az erős kölcsönhatás a magok stabilitását biztosítja; az atomot összetartó elektromágneses erő egy viszonylagos stabilitás mellett lehetővé teszi az élethez szükséges variabilitást is. A gyenge kölcsönhatás működteti a csillagokat, mint energiaforrásokat, egyúttal kiegyensúlyozza a gravitációs vonzást, hogy a csillagok idő előtti gravitációs kollapszusát is megakadályozza. Számtalan vizsgálatot végeztek annak kimutatására, hogy az intenzitások kis arányeltolódása milyen súlyos következményekkel járna.
 Külön érdemes megemlíteni, hogy Planck a 20. század első éveiben hogy jutott azokhoz a róla elnevezett tömeg-, idő-, hossz-értékekhez, amelyek végül a század utolsó éveiben kaptak komoly szerepet. Planck szavaival:
 „...a h és k konstans segítségével az a lehetőség adódik, hogy a hossz, a tömeg és az idő számára olyan egységeket határozzunk meg, amelyek függetlenül a speciális testektől és anyagoktól, jelentőségüket minden időkben,  minden, akár  földönkívüli, nem emberi kultúrák esetében is szükségszerűen megtartják és ezért joggal nevezhetők „természetes” mértékegységnek.
 A hossz, a tömeg, az idő... egységeit a már említett h és k, valamint (a fény terjedési sebessége a vákuumban), továbbá f (a gravitációs konstans) segítségével rögzíthetjük. Ezek értéke cgs egységekben

h = 6,548.10^-27 gcm²/s; k = 1,346.10^-16 gcm²/s² grad
c = 3·10¹⁰ cm/s;  f = 6,685.10^-8 cm³/gs².

Ha most már a „természetes egységeket” úgy választjuk, hogy az új rendszerben a felírt négy konstans mindegyikének értéke 1 legyen, akkor a következő egységeket kapjuk

                   = 4,03 . 10^-33 cm ;                             = 5,47.10^-5 g

                   = 1,34.10^-43 s 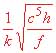                                   = 3,63·10³² grad

 Ezen értékek jelentőségüket megtartják mindaddig, amíg a gravitáció törvényei, a fény terjedési sebessége a vákuumban és a termodinamika két főtétele megmarad, tehát a legkülönbözőbb értelmes lény által a legkülönbözőbb módszerrel mérve, mindig ugyanazt az értéket szolgáltatják.

Az ábrán található rövidítések:
TOE = Theory of Everything (A Minden Elmélete), GUT = Great Unification Theory (A Nagy Egyesítési vagy Egységesítési Elmélet), QCD = Quantumchromodynamics (Kvantumszindinamika), QED = Quantumelectrodynamics (Kvantumelektrodinamika)
 

Most láthatjuk igazán, hogy a kozmológia és a részecskefizika mennyire  egymásra   vannak utalva.   Az elemi   rész fizika nélkül az
Ősrobbanás nem érthető meg és a kozmológia törvényeinek ismerete nélkül a részecskefizika alapfeltevéseinek helyessége nem igazolható.

 A 7. ábrán  a világ fejlődését látjuk az ősrobbanástól (Big Bang, Urknall) napjainkig megmutatva az egyes elméletek kompetenciájának határát.
 Az Ősrobbanástól napjainkig – az Univerzum életének minden thrillernél izgalmasabb drámája: megmagyarázásához, megértéséhez a 20. század fizikájának minden eredményét, annak összes matematikai eszköztárával együtt fel kell használni; ezen kívül az Univerzum, mint egyedi objektum még külön problémákat vet fel, elegendő munkát adva a 21. század fizikusainak is.

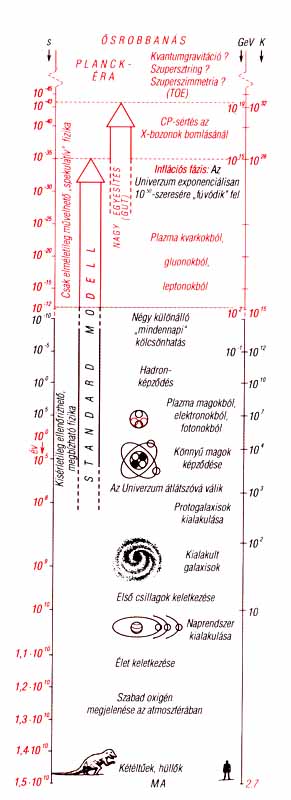
7. ábra. Az Ősrobbanástól napjainkig: az Univerzum élettörténete.
Egy ilyen ábra természetszerűen csakis elnagyolt lehet. A részletek ugyanis szerzőnként és évenként változnak. Itt csak a CP-sértéshez fűzünk megjegyzést, mert ez a fogalom nem szerepel a szövegben: végső fokon úgy tűnik, hogy ez a jelenség felel az anyag-antianyag asszimetriáért a világ jelenlegi állapotában. Az ötvenes évek nagy szenzációja volt, hogy a mikrovilág folyamatai nem szükségszerűen invariánsok tükrözéssel, vagy más néven P-transzformációval szemben (1956). Egy jelenség tükörképe tehát nem mindig ábrázol egy reális, megvalósítható folyamatot. Ha azonban a tükrözéssel együtt áttérünk az antirészecskére, tehát töltéskonjugációt, C-transzformációt hajtunk végre, akkor az együttes PC-transzformáció által kapott jelenség már realizálható. Később (1964) kiderült, hogy van CP-sértő folyamat is, ami annyit jelent, hogy a folyamat mérhetően másképp folyik le az antirészecske, mint a részecske esetében. A kezdetben egyenlő mennyiségben jelenlevő anyag-antianyag szimmetriája így megbomlik: a (közönséges) anyagrészecskék száma, – ha igen csekély mértékben is – megnő az antirészecskék számához képest. A részecskék és antirészecskék a későbbiekben páronként szétsugárzódnak és így végül is egyetlen anyagfajta marad.
 Egyébként elméletileg kimutatható (Lüders 1952, Pauli 1957), hogy a CPT-transzformáció, vagyis ha még az időtükrözést is figyelembe vesszük, mindig reális folyamathoz vezet.
 

 A dráma színpadát az általános relativitás elmélet adja a maga görbült, expandáló terével. A szereplők, a sztárok a fundamentális részecskék és a köztük levő „vonzások és taszítások”, közreműködésükkel pedig az atommagok, atomok, molekulák, mindennapi életünk ismerősei, majd a makrotestek, galaxisok, csillagok, bolygók lépnek színre. 10^-12 s időpontban a részecskék  (átlag)  energiája 100 GeV (~10¹⁵ K) körül van. Ez az az energia, amelyet földi laboratóriumokban még meg tudunk valósítani: az elmélet minden állítását innentől kezdve kísérletileg közvetlenül ellenőrizhetjük, a jelenségekre pedig négy, most már önállóan működő kölcsönhatás jól kidolgozott elméletét alkalmazhatjuk („megbízható” fizika).

 Az elképzelések helyességét a következő kísérleti bizonyítékok támasztják alá:

 1)  A tágulás üteme. 2) A  világegyetem könnyű  elemeinek   (H, He, Li)  koncentrációja.  3)  A  2,75 K  hőmérsékletnek  megfelelő
háttérsugárzás. Azonban mindezek a fontos tények valójában a gravitáció és a magfizika közötti tartomány fizikáját tükrözik. A részecskefizikai jelenségek közvetlen nyomait nem látjuk egyelőre.

 Az Univerzum úgy 100 000 éves korában, 5000 K körüli hőmérsékleten az atomok nem abszorbeálták a fotonokat, az Univerzum „áttetszővé” vált. Az ekkor kialakuló egyensúlyi sugárzás hűlt le a kiterjedés miatt 2,75 K-re.

 A nehézségek rögtön az életkor meghatározásánál jelentkeznek: 5 és 20 milliárd év közötti értékek adódhatnak különböző elképzelések és kísérleti adatoknak megfelelően. Sokan számolnak a 13,6·10⁹ év értékkel, amely a tágulási együttható (Hubble-konstans) 75 km/sMpc lineáris visszavetítéséből ered (Hubble-kor). Az ábrán 15·10⁹ évet vettünk fel.

 A legnagyobb rejtély  és kihívás magának a végtelen tömeg- és energiasűrűségű szinguláris pontnak a léte. A gravitációs erő vonzó és  azt várnánk, hogy inkább egy fekete lyukba tűnik el az anyag ilyen sűrűség mellett, minthogy robbanásszerűen tágulni kezdjen. Az elméleti fizikusok nem fogadják el azt a feleletet, hogy a kezdő feltételek adottak, olyanok, amilyenek; számítsuk a kezdő feltételekhez a kezdeti energiát is. Igen, de kiderül, hogy ezek a kezdeti feltételek igen finoman össze vannak hangolva – gondoljunk csak a kölcsönhatás csatoló tényezőinek finom szabályozására (6. ábra), de ide tartozik a térbeli homogenitás is: nem valószínű, hogy ezeket nekünk kell így beleraknunk, vagy így összehangolva teremtődtek. Valamiképpen tehát az elméletből ki kell adódni a kezdeti feltételeknek is.

 A Big-Bang elmélet továbbfejlesztésében a legnagyobb figyelmet az inflációs elmélet (Alan Guth 1980) érdemelte ki. A Nagy Egyesítés Elméletéből (GUT) kiindulva  kereste meg a taszító hatást, amelyet minthogy tömegek között hat, antigravitációnak lehet nevezni.

 A mértékszimmetrikus elméletekben, mint amilyen a GUT is, a vákuum állapot, a kvantummechnika interpretálásában, nagyon különös. A vákuum számára lehetséges a gerjesztett állapot. (Ez megfelel az anyag egy halmazállapotának, fázisának a szilárdtest fizikában.) Bár a gerjesztett vákuum „üres” marad olyan értelemben, hogy nincsenek benne részecskék, mégis hatalmas energiával és nyomással rendelkezik. A nyomás azonban különleges tulajdonságú, éspedig negatív... (feltéve, hogy az Univerzum az instabil állapotú fázisában van), és ennek következtében antigravitációs hatása van. Guth úgy okoskodott, hogy ha az univerzum a vákuum gerjesztett állapotában keletkezett, egyáltalán nem kellett, hogy egy nagy csattanással induljon, elég volt egy kis kvantum-szösszenet, ami az Univerzumot instabil állapotából kizökkentette. Az „antigravitáció” hatása az Univerzumot egy exponenciálisan növekvő expanzió fázisába vitte – ezt a fázist Guth inflációs fázisnak (inflationary phase) nevezte és ez már éppen a nagy csattanás [6].

 A kezdő feltételek problémáját ez az elmélet úgy oldja meg, hogy azok teljesen önkényesek lehetnek, az infláció minden esetben automatikusan beállítja azokat a finoman hangolt értékeket, amelyeket eddig kívülről vittünk be.

 Stephan Hawking viszont azt állítja, hogy a kvantum kozmológia kiküszöbölte a kezdeti feltételek szükségességét: az Univerzumnak nincs „eredete” annak ellenére, hogy az idő a múltban véges.

 Mások azt hirdetik, hogy a kvantumkozmológiában még az ilyesfajta állítást is lehet az  elmélet számára kidolgozott matematikai
eszköztár segítségével értelmezni: a világ a semmiből keletkezett, éspedig azért, mert a semmi instabil.

 Az elméleti fizikusokban mindenesetre erős a meggyőződés, hogy az emberi elme képes olyan absztrakt, a mindennapi fogalmainktól messze elrugaszkodó gondolati (logikai) struktúrákat létrehozni, amelyekkel a világunk keletkezésével kapcsolatos problémák adekvát módon tárgyalhatók, vagyis segítségükkel következtetések vonhatók le a „megbízható”, a mérő fizika számára is. Gondoljunk csak arra, hogy a Maxwell-egyenletek fogalmi rendszere a maga idejében mekkora kihívást jelentett még a legnagyobb kortárs elmék absztrakcióképessége számára is, a belőlük levonható következtetések, az elektromágneses hullámok viszont ma már a köztudatban élnek, ha nem is a megértés, de legalább a megszokás szintjén (3. idézet).

Irodalom
1. Katona Zoltán: Elemi részek. Gondolat Kiadó, Budapest, 1978
2. Kiss Dezső: Bevezetés a kísérleti részecskefizikába. Akadémiai    Kiadó, Budapest, 1990
3. Glashow, S. L.: Interactions. A Warner Communications Company, New York 1988
4. Feynman, R. P.: QED. The Strange Theory of Matter and Light. Princeton University Press, Princeton 1988
5. Davies, P. C. W.- Brown, J. (Editors): Superstrings. A Theory of Everything? Cambridge University Press, Cambridge 1988
6. Davies, P. C. W. (Editors): The New Physics. Cambridge University Press, Cambridge 1989
7. Meyers, R. A. (Editor): Encyclopedia of Modern Physics Academic Press, New York 1990

A szerző kedves kötelességének tartja, hogy megköszönje Patkós András egyetemi tanár értékes és értékesített észrevételeit.

* A szerzőt ezen cikk megírásánál kettős szándék vezette: egyrészt szeretné, ha a cikk önmagában is olvasható lenne, másrészt kiegészítő, aktualizált befejező résznek szánta „A fizika kultúrtörténete” könyv harmadik kiadásához.

---