A közös tömegközéppontjuk körül keringő két égitest gravitációs mezőjében Lagrange 1772-ben fedezett föl két olyan egyensúlyi pontot (L4, L5), amelyikbe egy harmadik kis testet helyezve, az a két égitesttel szinkronban együtt keringve nem változtatja meg relatív helyét. Csillagászok több ezer kis égitestet találtak a Nap–Jupiter, Nap–Mars, Nap–Neptunusz kettős rendszerek stabil egyensúlyi L4 és L5 Lagrange-pontjaiban. Amióta 1961-ben Kazimierz Kordylewski lengyel csillagász két halvány foltot észlelt a Föld-Hold rendszer L5 Lagrange-pontja környékén, azóta e képződményt Kordylewski-porholdnak hívják.
Sok csillagász azonban kétségbe vonta e porhold létét, mondván, hogy ha össze is gyűlne ott bolygóközi anyag, akkor a Nap zavaró gravitációs hatása gyorsan kisöpörné onnan. Egy képalkotó polariméterrel fölszerelt földi távcsővel új, polarizációs bizonyítékot találtunk a Föld–Hold rendszer L5 Lagrange-pontja körüli porhold létezésére. Miután a földi légkör és az állatövi fény zavaró hatásainak tulajdonítható minden lehetséges műterméket kizártunk, a mért polarizációs mintázatok az L5 pont körüli, bolygóközi részecskéken szóródó polarizált napfénynek voltak tulajdoníthatók. A Kordylewski-porhold most észlelt polarizációs jeleiből kiolvasható égi struktúra létét a Föld–Hold rendszer L5 pontja környékének számítógépes modellezésével kapott részecskeeloszlás hasonló szerkezete is alátámasztja. A porhold polarimetriai észlelése rehabilitálja Kordylewski méltatlanul elfeledett és sokak által megkérdőjelezett 1961-es úttörő fotometriai megfigyelését.
Porfelhők a Lagrange-pontokban
Tekintsünk két égitestet (egy csillagot és egy bolygóját, vagy egy bolygót és egy holdját), amelyek a közös tömegközéppontjuk körül körpályán keringenek egymás gravitációs terében. A velük együttforgó koordináta-rendszerben így mindkettő egy helyben áll. Keressük a keringési síkban azon pontokat, ahova egy harmadik, elhanyagolható tömegű kis testet helyezve, az egyensúlyban maradva szintén nem változtatja a helyét (azaz nulla a sebessége, miáltal a Coriolis-erő is zérus). Ez úgy lehetséges, hogy e kis testre a keringési középponttól sugár irányban kifelé mutató centrifugális erő egyensúlyt tart a két égitest által kifejtett gravitációs erők eredőjével, ami pont a keringési középpontba mutat.
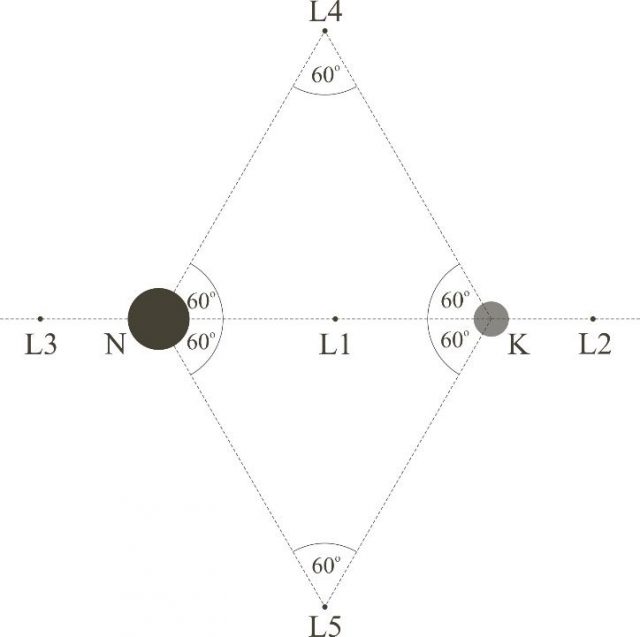
Ezen égi mechanikai probléma első részmegoldását 1767-ben Leonhard Euler (1707-1783) svájci matematikus-fizikus adta meg, amikor fölfedezte, hogy a két égitestet összekötő egyenesen három ilyen, kollineárisnak nevezett egyensúlyi pont (L1, L2, L3) is van. Ezek azonban instabilak, vagyis a bennük egyensúlyban lévő testet kissé kimozdítva, az soha sem tér vissza, hanem exponenciálisan növekvő mértékben eltávolodik. Az L1 pont a két égitest között van, az L2 pont a kisebb tömegű égitest nagyobbhoz képesti túloldalán helyezkedik el, míg az L3 pont a nagyobb égitest kisebbikhez viszonyított túloldalán (1. ábra). Joseph-Louis Lagrange (1736-1813) olasz-francia matematikus-fizikus 1772-ben talált további két, triangulárisnak hívott egyensúlyi pontot (L4, L5), amelyek a két égitest keringési síkjában egyik oldalával az őket összekötő egyenesen fekvő, az égitestek közti távolsággal megegyező két egyenlő oldalú háromszög egyenesen kívüli csúcsában helyezkednek el (1. ábra). Ha a két égitest Q = mkisebb/(mkisebb+mnagyobb) tömegaránya kisebb, mint Q* = 0,03852, akkor az L4 és L5 Lagrange-pontok lineárisan stabilak, mivel a bennük tartózkodó testet kissé kimozdítva, az a közelükben maradva ide-oda libeg, latinul librál (ekkor librációs pontokról beszélünk) [1]. Ha azonban Q ≥ Q*, akkor az L4 és L5 Lagrange-pontok instabilak az L1, L2 és L3 pontokhoz hasonlóan. Habár az L1, L2 és L3 kollineáris pontokat Euler fedezte föl, méltánytalanul ezeket is Lagrange-pontoknak nevezi a szakirodalom. Mivel a stabil L4 és L5 librációs pontokban csapdába esnek a megfelelő sebességű bolygóközi részecskék, ezért e jelenséget „Lagrange égi mechanikai porszívójának” hívjuk a továbbiakban.
Naprenszerünkben csillagászok nagyszámú kis égitestet találtak a bolygók és a Nap librációs Lagrange-pontjai körül. A legismertebbek a görög és a trójai kisbolygók a Nap-Jupiter rendszer L4 és L5 pontjai környékén [2]. Ugyancsak találtak kisbolygókat a Nap-Föld, Nap-Mars és Nap-Neptun rendszerek L4 és L5 pontjai körül.
De mi a helyzet a Föld és a Hold L4 és L5 Lagrange-pontjai környezetében? Mivel Q = mHold/(mHold+mFöld) = 0,012195 < Q* = 0,03852, ezért az L4 és az L5 pontok stabilak, miáltal a megfelelő sebességgel érkező bolygóközi részecskéket csapdába ejthetik. Ennek ellenére mégis lehetséges, hogy üresek e pontok a Nap zavaró gravitációs hatása miatt. A Nap e perturbációs hatását is figyelembe vevő kétdimenziós számítógépes modellezések [3, 4] azt mutatták, hogy ha egy részecskét elindítunk a Föld-Hold rendszer L5 pontja környékéről, akkor mozgása kaotikus lesz. Azonban sok olyan részecskepálya van, amely millió (106) napig sem hagyja el a rendszert, és akár 30-50 évig is megmaradó részecskecsomókat alkot az L5 pont körül. Ezért, bár a Nap csillagászati időskálán sok részecskét kisöpörhet a Föld–Hold L5 pontja környékéről, rövidebb időskálán sok a hosszú ideig az L5 pont közelében maradó részecske. E laza anyagtömörülést porholdnak nevezik.
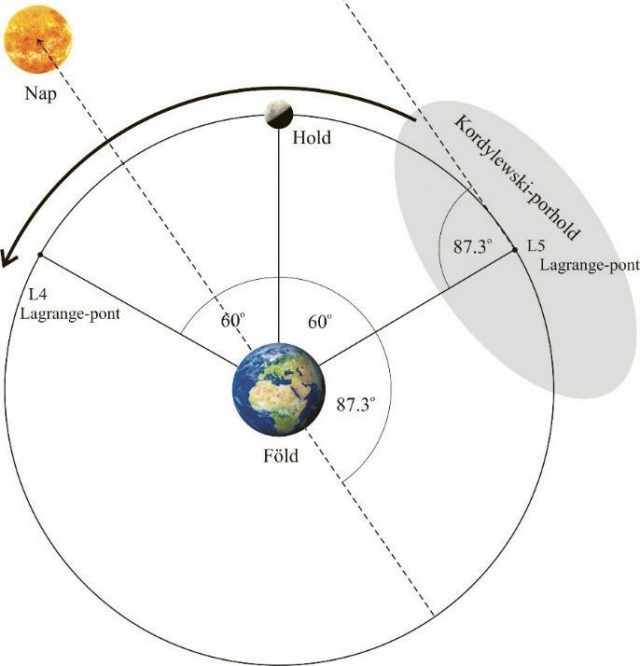
1961-ben Kazimierz Kordylewski lengyel csillagász szabad szemmel és távcsöves fényképezéssel is két halvány foltot észlelt a Föld-Hold rendszer L5 pontja környékén. Szerinte e foltok a napfénynek a csapdába esett bolygóközi poron történő szóródásával magyarázhatók [5]. E megfigyelés óta e képződményt Kordylewski-porholdnak nevezik (2. ábra). Kordylewski [5] úttörő fotometriai méréseinek Simpson [6], Vanysek [7], Roach [8] és Winiarski [9] csillagászok általi megerősítése ellenére sok más csillagász [10, 11, 12, 13, 14, 15, 16] azt feltételezi, hogy e porhold nem létezik, mert a Nap perturbációs hatása instabillá teszi a Föld–Hold rendszer L4 és L5 pontjait.
Hogy tisztázzuk a Kordylewski-porhold stabilitásának kérdését, számítógépes modellezéssel tanulmányoztuk a Nap, a Föld és a Hold, valamint 1 860 000 kistömegű részecske háromdimenzós mozgását. Feltérképeztük a Föld-Hold rendszer L5 pontja környékéről egy adott időn belül el nem szökő részecskék alkotta porhold méretét és alakját [17]. Mivel a Kordylewski-porhold létezését sok csillagász csak legendának tartotta, ezért képalkotó polarimetriával figyeltük meg a Föld és Hold L5 pontjának környékét [18]. Polarimetriai bizonyítékot találtunk az L5 körüli Kordylewski-porhold létezésére. Polarimetriai megfigyelésünket az L5 pont környékén képződő részecskefelhő számítógépes szimulációjával is alátámasztottuk [17].
Vita a Kordylewski-porhold létezéséről
Elméletileg a Kordylewski–porhold (KPH) a Föld–Hold rendszer L4 és L5 Lagrange-pontja körül kialakult kiterjedt, laza részecskesűrűsödés. Habár a bolygóközi por ilyen koncentrációjának lehetőségét a Nap–Föld rendszer L2 Lagrange-pontja közelében Moulton vetette föl 1900-ban [20], 1961. március 6. és április 6. között Kordylewski [5] fényképezett le először két, közel 6o kiterjedésű halvány foltot a Föld és Hold L5 pontja közelében a lengyel Kasprowy Wierchben, a Tátra-hegységben. Azóta e foltokat tekinti néhány csillagász a Kordylewskiporholdnak. De igen nehéz megkülönböztetni e porhold gyér fényét a Tejút fényétől, a csillagok fényétől, az állatövi fénytől és a légköri fényléstől [8]. Emiatt a KPH egymásnak ellentmondó több sikertelen és sikeres megfigyeléséről számoltak be csillagászok:
Sikertelen próbálkozások: 1966-ban és 1968-ban Roosen [10, 13] nem talált bizonyítékot a KPH létezésére a Föld–Hold rendszer L4 és L5 pontjában. 1967-ben Wolff és társai [12] az éjszakai égfényhez képest nem találtak 5 %-nál nagyobb többletfényt a Föld–Hold rendszer L4 és L5 pontjai közelében, annak ellenére, hogy egy repülőgépről készítettek fényképeket a csillagászati megfigyeléseknek kedvező körülmények között. Egy holdfogyatkozáskor 1969-ben Bruman [14] nem észlelte a KPH-t. Egy 1983-as fényképezési kutatásban Valdes és Freitas [15] egyetlen olyan librációs objektumot sem talált a Föld és Hold L4 és L5 pointjaiban, aminek fényessége meghaladta volna a 17-19 magnitúdót. Egyes vélemények szerint e kutatás fotometriája nem volt eléggé érzékeny az ennél is halványabb KPH észleléséhez. A kozmikus porrészecskék tömegének és sebességének mérésére tervezett, az ütközési ionizáció detektálásán alapuló Müncheni Por Számláló a japán Hiten űrszonda fedélzetén átvonult a Föld–Hold L4 és L5 pontján, de nem mért a környező űr porkoncentrációjánál nagyobb részecskesűrűséget [16].
Sikeres próbálkozások: 1969-ben Vanysek [7] a KPH szabad szemmel történő sikeres megfigyeléseiről tudósított. E megfigyelési kampányt 1966-ban a NASA végezte egy repülőgép fedélzetén négy alkalommal több tapasztalt megfigyelővel, akik a Föld–Hold rendszer L4 és L5 pontjai környékén igen halvány fénylésről számoltak be. A Rutgers OSO-6 Állatövi Fény Analizáló kísérlet adatainak elemzéséből Roach [8] 1975-ben arra következtetett, hogy a Föld és Hold L4 és L5 pontjai körül létezik a KPH, aminek 6o a szögkitérése a Földről nézve és e librációs pontok körül mozog. A Roztoki Górne megfigyelő állomáson több párhuzamos kamerát használva, 1989-ben Winiarski [9] azt tapasztalta, hogy a Föld–Hold rendszer L4 és L5 pontjai környéki Kordylewski-porholdak színe (spektruma) eltér az ellenfényétől (gegenschein: az állatövi fénynek a Nap ellenpontja közeli kifényesedése), ami azt jelzi, hogy a porholdakat alkotó részecskék összetétele és méreteloszlása különbözik az ellenfényt szóró bolygóközi porétól.
Számítógépes modellezés
A gravitációs négytest-probléma bizonyos eseteire vannak analitikus megoldások. Nemrég magyar csillagászok az égi mechanikai síkbeli szimmetrikus négytest-probléma („sárkány-alakzat”) azon speciális esetére találtak egzakt (azaz analitikus) megoldást [19], amikor a testekre ható erő a rendszer tömegközéppontjába mutat (centrális konfiguráció). Az új megoldás egy speciális esetben visszaadja a Lagrange-féle egyensúlyi pontokat. Azonban a négytest-probléma általános, közelítő, térbeli megoldása csak numerikus módszerekkel lehetséges. Ezért megalkottuk a Nap–Föld–Hold–porrészecske térbeli gravitációs négytest-probléma számítógépes modelljét, amit – változó lépésközű Runge–Kutta–Fehlberg integrátort alkalmazva – 1 860 000 részecskére egyenként lefuttattunk. Azt vizsgáltuk, hogy mely részecskék maradnak a Föld–Hold rendszer L5 Lagrange-pontja közelében tíz évig (3650 napig), vagyis van-e esély egyáltalán bármennyi anyagot is találni az L5 Lagrange-pont környékén. A gravitációs erő mellett a Napból érkező sugárnyomás és az úgynevezett Poynting–Robertson-effektus hatását is tanulmányoztuk, de e két utóbbi a gravitációhoz képest elhanyagolhatónak bizonyult 1 mikrométernél nem kisebb sugarú részecskék esetén.
Számítógépes modellezésünkkel azt találtuk, hogy a porrészecskék mozgása kaotikus, a Föld–Hold rendszer L5 pontja pedig képes több éven át is jelentős mennyiségű anyagot megtartani. Ezen anyagfelhő alakja folyamatosan változik, pulzál és örvénylik.
Bár a mi szimulációnk a Naphoz, Földhöz és Holdhoz képest elhanyagolható tömegű porrészecskékre történt, az eredmények 106 kg-ig gyakorlatilag ugyanazok voltak, ha eltekintettünk a porrészecskék egymásra gyakorolt gravitációs hatásától, ami megtehető. Ez azt jelenti, hogy akár sziklaméretű égitestek is sokáig (legalább tíz évig) az L5 pont közelében maradhatnak.
Polarimetriai vadászat
A Kordylewski-porholdat képalkotó polarimetriával észleltük, aminek során a vizsgált égterületről egymás után három fényképet készítettünk egyenként 180 másodperces expozíciós idővel egy lineáris polárszűrőn (Edmund Optics, 43-785, USA) át annak egymáshoz képest 120o-kal elforgatott három eltérő áteresztési iránya mellett. A mérés Slíz-Balogh Judit csillagászati magánobszervatóriumában történt Badacsonytördemicen (keleti hosszúság 17o 28’ 15”, északi szélesség 46o 48’ 27”) egy Moravian G3-11000 ABG CCD kamerára szerelt Tokina AF 300/2.8 teleobjektívvel, aminek látószöge 7,5o (vízszintes) × 5o (függőleges). Cikkünkben minden mérésnél a második polarizációs fénykép középidejét adtuk meg a mérés időpontjaként. A polarizációs felvételeket Barta András AlgoNet (http://www.estrato.hu/algonet) szoftverével értékeltük ki, ami kiszámította a p polarizációfokot és az α polarizációszöget a látható spektrum vörös (650 nm), zöld (550 nm) és kék (450 nm) tartományában. Az így kapott p és α értékeket hamisszínes kétdimenziós térképeken ábrázoltuk a három színcsatornában.
Polarizációs méréseinket a Föld–Hold rendszer L5 pontja körüli 7,5o×5o-os szögtartományban végeztük, amikor (i) az ég felhőtlen volt, (ii) a vizsgált égterületet vékony cirrus fedte, és (iii) amikor repülőgép kondenzcsík zavarta meg a felvételt. Kontrollként ugyanezt az égterületet vizsgáltuk a Bika csillagképben akkor is, amikor az L5 pont nem volt azon a területen. E méréssel az igen gyenge állatövi fény esetleges polarizációs hatását ellenőriztük. Az állatövi fény az ekliptika menti fényjelenség, amit a Naprendszert kitöltő bolygóközi anyag porszemcséin szóródó/visszaverődő napfény okoz.
Polarizációs portré
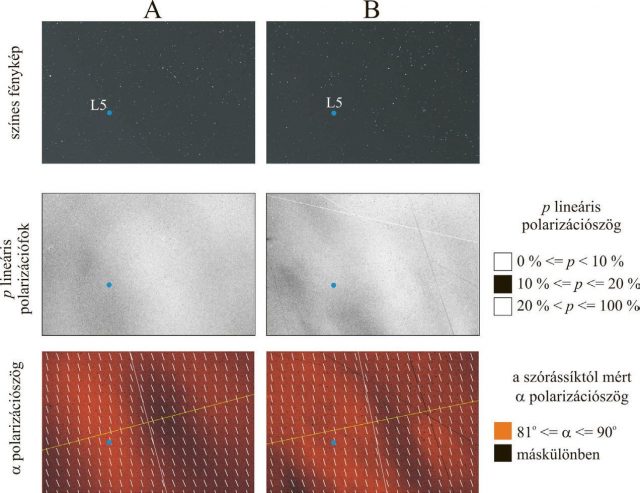
A 3A ábra a Kordylewski-porhold 2017. augusztus 17-én 23:29:67 csillagászati világidőkor (UT) képalkotó polarimetriával mért optikai információit mutatja 73o fázisszög mellett. A spektrum zöld (550 nm) tartományában mért p polarizációfok-mintázaton jól elkülöníthető két diffúz halmaz, amelyek fekete képpontjai 10 % ≤ p ≤ 20 % közötti polarizációfokot jelölnek. Az egyik halmaz az L5 pont körül, míg a másik tőle jobbra található. A polarizációszög-mintázaton vörös szín jelöli a 81o ≤ α ≤ 90o közötti polarizációszögű pontokat. A spektrum vörös (650 nm) és kék (450 nm) tartományában a 3A ábráéhoz teljesen hasonló mintázatokat kaptunk. Fontos hangsúlyozni, hogy a polarizációszög mintázatán a polarizációirányt jelző kis fehér pálcikák majdnem teljesen merőlegesek a hosszú sárga vonallal jelölt szórási síkra. Ez minden fényszórási folyamatra jellemző, ezért ez az egyik legfontosabb bizonyíték arra, hogy az L5 pont körül sok fényszórócentrum létezik, amelyek nem lehetnek mások, mint a Kordylewski-porhold részecskéi, mert az állatövi fény hatását kontrollmérésekkel kizártuk.
A 3B ábra az L5 pont körüli Kordylewski-porhold képalkotó polarimetriával mért p– és α-mintázatait mutatja a spektrum zöld (550 nm) tartományában 2017. augusztus 19-én 01:14:15 világidőkor 87,3o fázisszög mellett. E porhalmaz jellemzői hasonlóak a 3A ábra kétrészes porhalmazéihoz, eltekintve attól, hogy ezúttal ötrészes a porstruktúra. E struktúraváltozás szerint tehát a porhold sajátságai idővel változnak. Ilyen többrészes dinamikus struktúrát kaptunk a számítógépes szimulációval is (lásd később).
Azon lehetőség ellenőrzése érdekében, hogy a Kordylewski-porhold helyett a polarizációérzékeny teleszkópunkkal esetleg valami műterméket vagy az állatövi fényt észleltük volna, kontrollméréseket végeztünk. Ezekkel kizártuk, hogy valamilyen mechanikai vagy optikai tárgyról a teleszkópunkba verődő fényt, esetleg egy vékony fátyolfelhő vagy egy repülőgépkondenzcsík szórt fényét mértük volna. Az állatövi fény mérésének eshetőségét úgy ellenőriztük, hogy akkor is mértünk, amikor az L5 pont nem volt a korábban vizsgált égterületen, s ekkor gyakorlatilag nulla polarizációfokokat mértünk s a polarizációirányok sem voltak merőlegesek a szórási síkra, vagyis semmiféle szórócentrumsűrűsödésre utaló jelet sem találtunk. Minden más kontrollmérés is a Kordylewski-porhold polarizációs mintázataitól teljesen eltérő eredményekre vezetett.
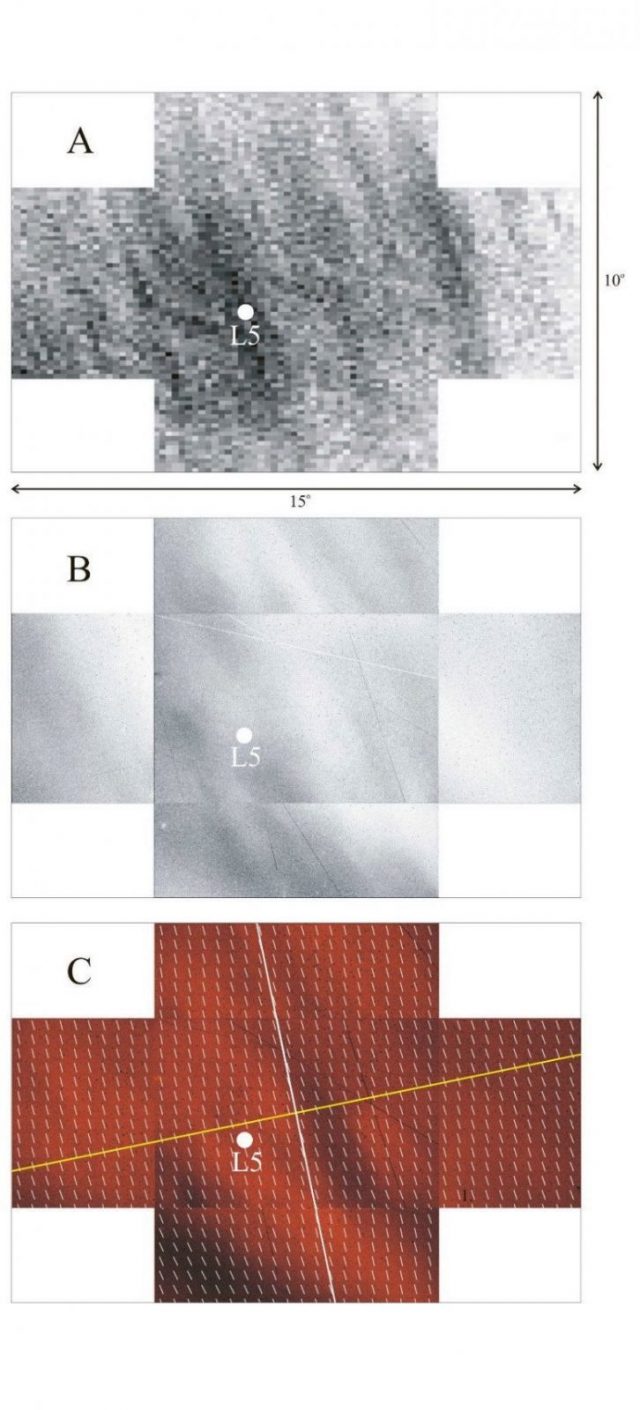
A 4A ábra az L5 pontban összegyűlt porrészecskék számítógépes szimulációval kapott sűrűségeloszlását mutatja azon égterületen, amely megfelel a távcsöves képalkotó polarimetriával vizsgált égtartománynak. A 4B és 4C ábra a Kordylewski-porhold 2017. augusztus 19-én mért p polarizációfok- és α polarizációszög-mintázatait szemlélteti a spektrum zöld (550 nm) tartományában. Ha összehasonlítjuk a számítógépes modellezéssel kapott részecskeeloszlást a mért polarizációs mintázatokkal, akkor feltűnő hasonlóságot tapasztalunk: mindhárom mintázaton több elnyúlt csomósodás látszik, amelyek a Kordylewski-porhold heterogén szerkezetét demonstrálják. A szomszédos égi ablakokbeli polarizációs mintázatokat nem lehetett tökéletesen egymáshoz illeszteni, mert a polarimetriai mérések a szomszédos ablakokban 3×180 másodperces késéssel történtek az exponálásnak köszönhetően, és e rövid idő alatt is kis mértékben változott a porhold szerkezete.
Tehát képalkotó polarimetriával első alkalommal sikerült megfigyelni és rögzíteni a Föld–Hold L5 Lagrange-pontja körüli Kordylewski-porholdat. Ezzel megerősítettük e Földet kísérő laza szerkezetű égitest létezését és rehabilitáltuk Kordylewski úttörő megfigyelését [5]. Az 5. ábra az éjszakai csillagos eget szemlélteti a Föld–Hold rendszer L5 Lagrange-pontja környékén lévő Kordylewski-porholddal, a Földdel, a Holddal és a Nappal.
A porhold megfigyelhetősége
A számítógépes szimulációk szerint a Kordylewski-porhold inhomogén, dinamikus, időben változó részecskesűrűségű. Mivel e porfelhőt közvetlenül a Nap világítja meg, ezért a napfény szóródik a porrészecskéken, mely igen halvány szórt fény elegendően érzékeny detektorokkal vagy szabad szemmel a Föld felszínéről is megfigyelhető. Elsőként Kordylewski [5] készített ilyen úttörő fényképekete porfelhőről. Fotometriával vagy szabad szemmel [7, 8, 9] a Kordylewski-porhold csak kis fázisszög alatt (amit a Nap, az L4/L5 pont és a megfigyelő határoz meg, 1. ábra) figyelhető meg, vagyis „teliporhold” esetén. Ekkor azonban a p polarizációfok minimális, gyakorlatilag nulla. A polarizációfok 90o fázisszögnél maximális, vagyis ekkor van a legnagyobb esély arra, hogy a Kordylewsky-porholdat polarimetriával észleljük. Mi 90o-hoz közeli fázisszögek mellett észleltük e porhold polarizációs jeleit (3. ábra).
Az elmélet szerint a poron szóródó napfény a Nap, a földi megfigyelő és a szórócentrum által meghatározott síkra merőleges irányban részlegesen polarizálttá válik. És valóban, ezt az előre várt polarizációs jellemzőt találtuk a képalkotó polarimetriás méréseinkkel (3. ábra, 4B és 4C ábra), de csak akkor, ha az L5 pont a távcső látómezejébe esett. Ez a legerősebb bizonyíték arra, hogy a Föld légkörén kívüli napfényszóró felhőt (de nem az állatövi fényt!) észleltünk, nem pedig földi eredetű jelenséget. További bizonyíték a Kordylewski-porhold létére, hogy a polarizációs mintázatokon ugyanolyan többrészes csomósodás figyelhető meg, mint amit a számítógépes szimuláció eredményezett.
Elméletileg minél közelebb van a szórási szög 90o-hoz, a szórt fény p polarizációfoka annál nagyobb. És valóban, azt találtuk, hogy a Kordylewski-porhold 2017. augusztus 19-én 87,3o fázisszög mellett mért p-értékei nagyobbak, mint a 2017. augusztus 17-én mértek, amikor a fázisszög 73o volt. Ez még egy érv amellett, hogy polarimetriával a Kordylewski-porholdat figyeltük meg, nem pedig egyéb jelenséget.
Számos példa igazolja, hogy a csillagászati információk megszerzésében mennyire hasznos módszer a (képalkotó) polarimetria. A polárszűrőkkel fölszerelt távcsövekkel vizsgálható például a Föld légköre, a napkorona, a Naprendszer bolygóinak és holdjainak felszíne, a távoli csillagok, galaxisok és ködök. A csillagászokhoz az égi információ nagy része a fényen keresztül érkezik. E fény jöhet közvetlenül a Napból. A napfény polarizálatlan, de amint útja közben bolygóközi poron vagy a légkör részecskéin szóródik, lineárisan polárossá válik. Mivel a hosszabb hullámhosszak kevésbé szóródnak, mint a rövidebbek, és a Kordylewski-porholdat az általa szórt napfény alapján észleljük, ezért fotometriai észlelése az infravörös tartományban még nehezebb, mint a láthatóban.

Lagrange-pontja közelében.
Csillagászati és űrkutatási jelentőség
A Föld-Hold rendszer L4 és L5 Lagrange-pontjai bolygóközi porszívó hatásának (stabilitásának) fontos szerepe lehet. Alkalmas például űrhajók, műholdak és űrtávcsövek minimális energiabefektetésű állomásoztatására. Jelenleg azonban nincs űreszköz a Naprendszerben sehol sem az L4 és L5 pontok körül. Mindkét pont átszálló állomás lehet a Marsra vagy más bolygókra indított űrexpedíciók számára, valamint állomásai lehetnek az úgynevezett bolygóközi szupersztrádának. Az utóbbi olyan optimális pálya, amin minimális üzemanyagfelhasználással mozgathatók űreszközök a bolygók gravitációs lendítő erejét kihasználó hintamanőverek sorozatával. Az is lehetséges, hogy a Föld légköréből kivont fagyasztott széndioxidot a Föld–Hold stabil L4 és L5 Lagrange-pontjába lőjük, hogy megszabaduljunk az üvegházhatást okozó fölösleges szén-dioxidtól. Végül, a Kordylewski-porhold dinamikájának vizsgálata fontos az űrhajózás biztonsága szempontjából is, hogy elkerülhessük űreszközeinknek a porhold részecskéivel történő ütközéseit.
SLÍZ-BALOGH JUDIT – BARTA ANDRÁS – HORVÁTH GÁBOR
![]() Köszönetnyilvánítás: Köszönjük Slíz Miklósnak (Graphisoft, Budapest) és Mádai Attilának (Érd) a számítógépes modellezésben és a távcsőépítésben nyújtott programozói és mérnöki segítségüket.
Köszönetnyilvánítás: Köszönjük Slíz Miklósnak (Graphisoft, Budapest) és Mádai Attilának (Érd) a számítógépes modellezésben és a távcsőépítésben nyújtott programozói és mérnöki segítségüket.
IRODALOM
[1] Szebehely V. (1967) Theory of Orbits: The Restricted Problem of Three Bodies. Academic Press, New York
[2] Schwarz R., Dvorak R. (2012) Trojan capture by terrestrial planets. Celestial Mechanics and Dynamical Astronomy 113: 23-34
[3] Slíz J., Süli Á., Kovács T. (2015) Control of chaos in the vicinity of the Earth-Moon L5 Lagrange point to keep a spacecraft in orbit. Astronomical Notes 336: 23-31
[4] Slíz J., Kovács T., Süli Á. (2017) Chaos control with ion propulsion. Astronomical Notes 338: 536-549
[5] Kordylewski K. (1961) Photographische Untersuchungen des Librationspunktes L5 im System Erde-Mond. Acta Astronomica 11: 165-169
[6] Simpson J. W. (1967) Dust cloud moons of the Earth. Physics Today 20: 39-46
[7] Vanysek V. (1969) Detectability of lunar libration clouds at small phase angles. Nature 221: 47
[8] Roach J. (1975) Counterglow from the Earth-Moon libration points. Planetary and Space Science 23: 173
[9] Winiarski M. (1989) Photographic observations of the clouds in the neighbourhood of libration point L5 of the Earth-Moon system. Earth, Moon and Planets 47: 193-215
[10] Roosen R. G. (1966) A photographic investigation of the point in the Earth-Moon System. Sky & Telescope 32: 139
[11] Roosen R. G., Harrington R. S., Jeffreys W. H. (1967) Doubt about libration clouds. Physics Today 20: 9-11
[12] Wolff C., Dunkelman L., Hanghney L. C. (1967) Photograph of the Earth’s cloud satellite from an aircraft. Science 157: 427-429
[13] Roosen R. G. (1968) A photographic investigation of the gegenschein and the Earth-Moon libration point. Icarus 9: 429-439
[14] Bruman, J. R. (1969) A lunar libration point experiment. Icarus 10: 197-200
[15] Valdes F., Freitas R. A. Jr. (1983) A search for objects near the Earth-Moon Lagrangian points. Icarus 53: 453-457
[16] Igenbergs E. et al. (2012) Chapter 9: The Munich dust counter – A cosmic dust experiment on board of the Muses-A mission of Japan. pp. 45-48. In: Origin and Evolution of Interplanetary Dust. (editors: A. C. Levasseur-Regourd, H. Hasegawa) Kluwer Academic Publishers
[17] Slíz-Balogh J., Barta A., Horváth G. (2018) Celestial mechanics and polarization optics of the Kordylewski dust cloud in the Earth-Moon Lagrange point L5 – Part I. Three-dimensional celestial mechanical modelling of dust cloud formation. Monthly Notices of the Royal Astronomical Society 480: 5550-5559
[18] Slíz-Balogh J., Barta A., Horváth G. (2018) Celestial mechanics and polarization optics of the Kordylewski dust cloud in the Earth-Moon Lagrange point L5 – Part II. Imaging polarimetric observation: new evidence for the existence of Kordylewski dust cloud. Monthly Notices of the Royal Astronomical Society 482: 762-770
[19] Érdi B., Czirják Z. (2017) Central configurations of four bodies with an axis of symmetry. Celestial Mechanics and Dynamical Astronomy 125: 33-70
[20] Moulton F. R. (1900) A meteoric theory of the Gegenschein. Astronomical Journal 21: 17-22
A cikk a Természet Világa 2019. áprilisi számában (150. évf. 4. sz.) jelent meg.


