Eötvös Loránd és munkatársai 1906-tól több méréssorozatot végeztek a súlyos és a tehetetlen tömeg azonosságára vonatkozó ekvivalencia-elv igazolására. Ugyan Einstein általános relativitáselméletének kiinduló alappillére, mégis az ekvivalencia-elv a mai napig vitatott kérdése a fizikának. A XVI. századtól kezdve többen is foglalkoztak erre vonatkozó kísérletekkel, és például azt tapasztalták, hogy vas és fagolyó egyidejű ejtésekor a két test a nagy súlykülönbség ellenére gyakorlatilag egyszerre ért a talajra. Később Newton és Bessel már kimondottan a súlyos és tehetetlen tömeg ekvivalenciáját tesztelték különféle ingákkal végzett kísérletekben. Az ekvivalencia-elvet végül Eötvös Loránd és munkatársai bizonyították igen nagy pontossággal, azonban az ő méréseik után is maradt nyitott kérdés.
Newton II. törvénye szerint bármely testre ható erő egyenlő a test tömegének és a gyorsulásának szorzatával (F = ma), vagyis bármilyen mechanikai erőhatás is éri a testet (lehet ez rugóerő, súrlódási erő, vagy akár nehézségi erő), az erő és a gyorsulás hányadosa mindig ugyanannyi, a testre jellemző mennyiség, a tehetetlen tömeg. Van ugyanakkor egy erő, ami bármely két test között mindig fellép. Ez a vonzóerő a jól ismert Newton-féle általános tömegvonzási (gravitációs) erő, melynek nagysága szintén arányos a testre jellemző mennyiséggel, a súlyos tömeggel. A súlyos és a tehetetlen tömeg egymástól független mennyiség, ami két teljesen különböző fizikai törvényben jelenik meg. Newton óta a fizika kiemelt kérdése, hogy a két tömeg valójában ugyanaz-e, vagy más-más mennyiséget jelöl.
A kétfajta tömeg azonosságának igazolására a legenda szerint elsőként Galilei 1586-ban végzett látványos kísérletet a pisai ferde toronyban, ahol különböző anyagokat ejtett le, és a talajra érkezésük egyidejűségét vizsgálta (1. ábra). (A kísérletet egyébként nagy valószínűséggel nem Galilei, hanem korábban Simon Stevin, és nem a pisai ferde toronyban, hanem a hollandiai Delftben végezte.) A kísérlet alapkérdése az volt, hogy vajon anyagfüggő-e a gravitáció. Az ejtési kísérlet fizikai alapelvét megfontolva könnyen megérthetjük a súlyos és a tehetetlen tömeg azonosságának kérdését.
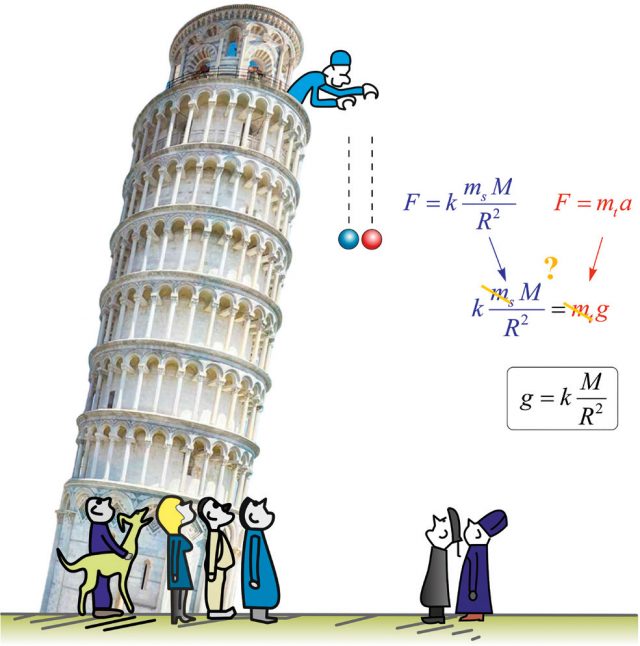
Különböző tömegek között a Newton-féle általános tömegvonzási erő (F) hat, amelynek nagysága arányos a Föld M és az ejtett próbatest ms súlyos tömegével és fordítva arányos a tömegközéppontjaik közötti R távolság négyzetével. A jól ismert összefüggés az 1. ábrán látható, amelyben a gravitációs állandót k-val jelöltük. Ugyanakkor Newton II. törvénye értelmében a testek erő hatására gyorsuló mozgást végeznek, az a gyorsulás arányos a tömegre ható F erővel és fordítottan arányos a test mt tehetetlen tömegével. Elhanyagolva most a forgási centrifugális erőt és az árapály erőket, a szabadon eső testek a = g gyorsulását éppen a Newton-féle tömegvonzási erő okozza, így a két egyenlet az 1. ábrán látható módon egyenlővé tehető egymással. Amennyiben az egyenlőség két oldalán a súlyos ms és a tehetetlen mt tömeg egyenlő egymással, akkor egyszerűsíthetünk velük, és végeredményként azt kapjuk, hogy a g gyorsulás csak a Föld M tömegétől és az R földsugártól függ, vagyis független a szabadon eső testek tömegétől és anyagától. A tapasztalat szerint az ejtési kísérletben a különböző anyagok egyszerre értek a talajra, ami az akkori szerény pontossággal azt mutatta, hogy a súlyos és a tehetetlen tömeg azonosak.
Nagyjából 300 évvel később, Eötvös Loránd először 1889-ben, az addigi méréseknél több nagyságrenddel pontosabb kísérleteket végzett, majd később 1906-tól az akkori technikai lehetőségeknek megfelelően a híres Eötvös– Pekár–Fekete(EPF)-kísérlettel a kilencedik tizedesjegyig terjedő pontossággal igazolta a súlyos és a tehetetlen tömeg azonosságát [1].
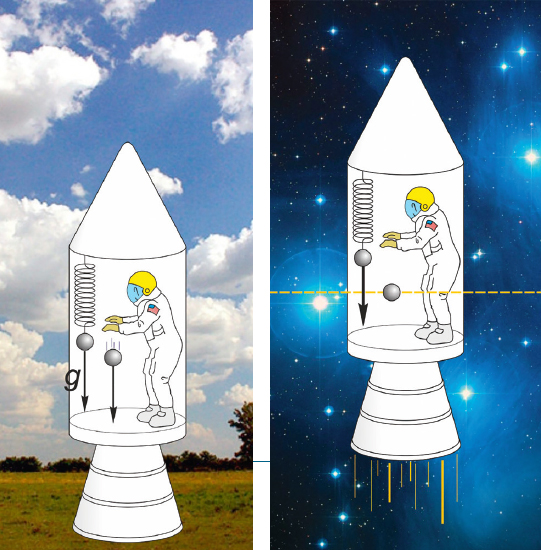
Einstein a súlyos és a tehetetlen tömeg egyenlőségére és anyagtól való függetlenségére, vagyis az ún. gyenge ekvivalencia-elvre építette fel általános relativitáselméletét. A gravitációs (súlyerő) és a tehetetlenségi erő érzékeltetésére Einstein gondolatkísérletet alkotott, melynek az a lényege, hogyha egy fizikust bezárunk egy kabinba, felruházzuk az emberiség teljes fizikatudásával és a rendelkezésére bocsátunk minden elképzelhető fizikai eszközt és kísérleti lehetőséget, akkor sem képes megállapítani, hogy a kabin gravitációs erőtérben nyugszik, vagy az univerzum távoli gravitációs tömegektől mentes területén rakétahajtómű gyorsítja (2. ábra). A helyzet azonban nem ilyen egyszerű; ma már tudjuk, hogy méréssel mégis különbséget lehet tenni a két erőtér között. Ha ugyanis egyszerű rugós graviméterrel két különböző alkalmas pontban mérünk, akkor gravitációs erőtérben a vonzó tömegtől mért távolság függvényében különböző értékeket fogunk észlelni, ugyanakkor gyorsuló erőtérben, különböző pontokban nem tapasztalunk különbséget. Szaknyelven fogalmazva: a gravitációs erőtérnek van gradiense, a gyorsuló erőtér viszont homogén. Ez is arra utal, hogy a súlyos és a tehetetlen tömeg azonosságának kérdése egyáltalán nem egyszerű probléma.
Az Eötvös-féle ekvivalencia-mérések
Eötvös Loránd és munkatársai, Pekár Dezső és Fekete Jenő 1906-tól több méréssorozatot végeztek a súlyos (gravitációs) és a tehetetlen tömeg arányosságára vonatkozóan. A méréseiket arra alapozták, hogy a földi nehézségi erő a tömegvonzási és a forgási centrifugális erő eredője, és amennyiben a gravitációs erő anyagfüggő, akkor az eredő nehézségi erő iránya szintén az lesz, ami egy K−Ny tájolású Eötvös-ingával kimutatható. Az elvégzett mérések csupán 10-9 hibahatár közeli véletlenszerűnek tűnő eltéréseket mutattak.
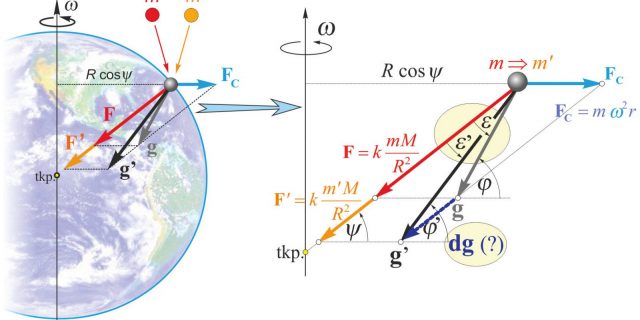
A g földi nehézségi erő három összetevője az FT tömegvonzási erő, a Föld tengelykörüli forgásából következő Fc centrifugális erő és az árapálykeltő erők eredője. Az EPF-kísérletek során az árapálykeltő erők elhagyhatók, mivel a kísérletben használt eszközre kifejtett hatásuk kicsi. Eötvös feltételezte, hogy az Fc forgási centrifugális erő független az anyagi minőségtől, az FT tömegvonzási erő viszont függhet tőle. Gondolatban helyezzünk el a 3. ábrán látható földfelszíni pontban különböző anyagokat, például aranyat és alumíniumot. A két különböző testnek legyen szigorúan azonos a tömege (m = m’). A feltételezés szerint mindkét testre azonos Fc forgási centrifugális tehetetlenségi erő hat, viszont a Föld az m tömegre FT, míg az m’ tömegre FT’ gravitációs erőt gyakorol. Ennek megfelelően a 3. ábrán látható módon az m tömegre ható nehézségi erő g, az m’ tömegre ható nehézségi erő pedig g’. Amennyiben a gravitáció anyagfüggő, a g és a g’ közötti parányi dg különbség tapasztalható, mely Eötvös-ingával mérhető.
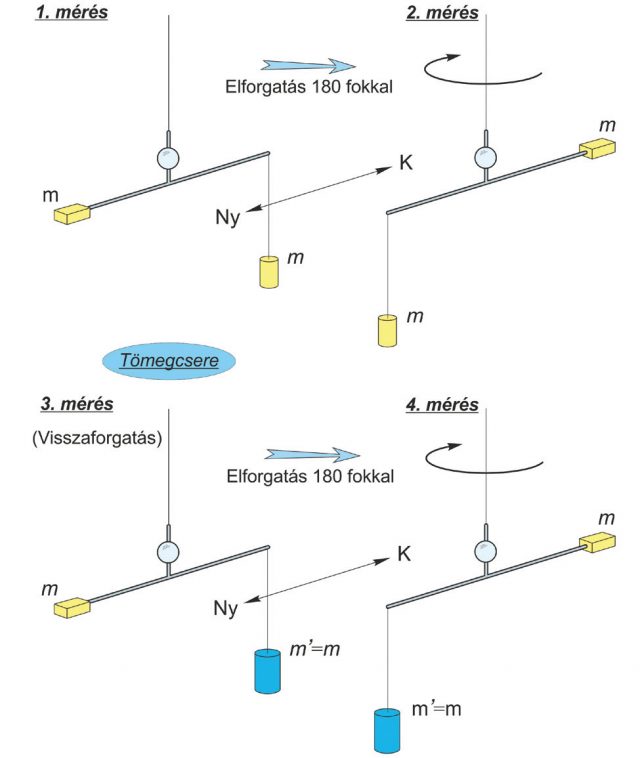
Az ekvivalencia-kísérletben az Eötvös-inga megfelelő forgatásával és a tömegek meghatározott cseréjével a 4. ábrán összefoglalt stratégia szerint történnek a mérések.
Az első lépésben a K−Ny irányba beállított ingaszerkezeten leolvassuk az ingarúd nyugalmi helyzetét. A második lépésben 180 fokkal elfordítjuk az ingaszerkezetet és itt is leolvassuk az ingakar nyugalmi helyzetét. A harmadik lépésben visszaforgatjuk az ingaszerkezetet K−Ny irányba, az inga lelógatott aranyból készült tömegét kicseréljük egy ugyanolyan tömegű más, például alumínium tömegre, majd a nyugalmi állapotban ismét leolvassuk az ingakar nyugalmi helyzetét. Végül a negyedik lépésben a felcserélt tömeggel is elfordítjuk az ingaszerkezetet 180 fokkal és így is leolvassuk az ingakar nyugalmi helyzetét. A súlyos és a tehetetlen tömeg különbözősége esetén a felcserélt tömegekkel kissé megváltozna az ingakar nyugalmi pozíciója. A valóságban a mérési stratégia ennél bonyolultabb, mivel kettős-ingákkal mérünk, és egyetlen Eötvös-ingában 180 fokkal ellentétes pozícióban két független ingaszerkezet működik [2, 3].
Eötvösék az ekvivalencia-mérésekhez a legkülönbözőbb anyagokat, például platina, magnálium (Mg-Al ötvözet), kígyófa, réz, azbeszt, faggyú, víz, rádium-bromid, rézszulfát-pentahidrát, stb. használtak. A mérések során jelentős különbséget egyetlen anyagpárra sem találtak, így 10-9 pontossággal igazolták a súlyos és a tehetetlen tömeg azonosságát. A mérésekben azonban tapasztalhatók parányi nyugtalanító eltérések. Renner János az 1930-as években más anyagpárokkal megismételte a kísérletet, de anyagfüggést ő sem talált.
Később, 1986-ban Fischbach és munkatársai az említett eltéréseket vizsgálva arra a következtetésre jutottak, hogy ezek nem teljesen véletlenszerűek, hanem az atommagok kötési energiájának lineáris függvényeként írhatók fel, és felvetették egy rövid hatótávolságú, úgynevezett ötödik erő létezését [4]. Az ötödik erő szerintük a gravitációnál lényegesen gyengébb, a barionok (protonok és neutronok) számával arányos, és hatótávolsága néhány tíz vagy száz méter. A feltételezés komoly vitákat váltott ki, és további méréseket és ellenőrző kísérleteket motivált. Eötvösék eredményeit részletesen elemezték, új, sokkal pontosabb méréseket is végeztek, de azokban nem mutatták ki a megjósolt Yukawa-jellegű, rövid hatótávolságú ötödik erőt. További más kísérletek során Dicke és munkatársai 10-11, Braginsky és társai pedig 10-12-es pontossággal igazolták az ekvivalencia-elvet. Dicke és munkatársai északdél tájolású ingával a Nap tömegvonzása és a Föld keringéséből adódó keringési centrifugális erő viszonyának anyagfüggését mérték, aminek előnye, hogy az ingát, a jel 24 órás periodicitása miatt a mérés során nem kellett forgatni.
Az ekvivalencia-kísérlet újramérése
Az EPF-kísérletben vizsgált ekvivalencia-elv ma újra a kutatások homlokterében áll, a torziós inga továbbra is fontos kérdések eldöntésére alkalmas. 2017-ben fizikus kollégákkal úgy gondoltuk, hogy Eötvös Loránd halálának 100 éves évfordulója tiszteletére a mai modern technikai adottságokat kihasználva megismételjük az ekvivalencia-méréseket. Elhatározásunk akkor vált különösen indokolttá, amikor az előkészületek során tanulmányozva az eredeti méréseket megfejtettük a szabályos eltérések nagy valószínűségű okát. Vizsgálataink szerint az ekvivalencia-mérésekben tapasztalható parányi szabályos eltérés abból adódhat, hogy a próbatest méretével összevethető távolságon a nehézségi erő megváltozása már nem tekinthető egyenletesnek, így a kísérlet eredményét befolyásolja a próbatestek alakja is [5]. Eötvösék méréseiben a felhasznált különböző sűrűségű, henger alakú próbatestek térbeli kiterjedése, magassága lényegesen eltérő volt, például a platina henger 6 cm, a magnálium henger 11,9 cm, a kígyófából készült henger pedig már 24 cm magas volt. Olyan nehézségi erőtérben (például vastag falak közelében), ahol az erőtér változása rövid távolságon belül is jelentős, a kisebb kiterjedésű testekre más erő hat, mint azokra, amelyek nagyobb kiterjedésük miatt más térerősségű helyre is benyúlnak. Az eredeti ekvivalenciakísérlet annyira érzékeny volt, hogy már egy ilyen kicsiny másodrendű gravitációs hatás is megjelenhetett az eredményekben, amire Eötvösék akkor nem gondoltak.

A tervezett mérések céljára az 5. ábrán látható két különböző típusú Eötvös-inga jöhetett szóba: egy Eötvös–Rybár-féle AutERBal-inga és egy Eötvös–Pekár-féle ún. kettős kis eszköz. Mindkét rendelkezésünkre álló műszert az 1930-as években terepi mérések céljára készítették. Az AutERBal-inga fotóregisztrálással teljesen automatizáltan működött, speciális óraszerkezet vezérelte, a Pekár-inga nem automatizált, tapasztalatunk szerint megbízhatóbb és pontosabb műszer. Első fontos feladatunk az ingák felújítása, javítása, használhatóságuk ellenőrzése, a mai modernebb technikai lehetőségeknek megfelelő átalakítása és kalibrálása volt. Az előkészületek közel 2 évet vettek igénybe. A torziós szálak csavarodási driftjének minimálisra csökkentése céljából a szálakat több mint fél éven keresztül folyamatosan terheltük az ingák kioldott helyzetében. A szálak hosszú idejű terhelésével a Pekár-inga esetében sikerült elérni mindkét szál gyakorlatilag driftmentes állapotát, így az igen nagy pontossági igényű mérések céljára a Pekár-inga használata mellet döntöttünk. Ráadásul mivel az Eötvös-kísérlet tekintetében fontos szempont az ingában lévő tömegek egyszerű cserélhetősége is, ezért a további fejlesztéseket már csak erre az eszközre koncentráltuk.
A sikeres mérések legfontosabb követelménye a zavaró körülmények minél teljesebb kiiktatása. Az Eötvös-kísérlet méréseit leginkább veszélyeztető hibaforrások a műszert leolvasó személy zavaró tömege, a talajrezgések, a hőmérséklet változása és a nehézségi erőtér gradienseinek magas értéke az inga környezetében. Utóbbi probléma egyszerűen kezelhető megfelelő mérési helyszín kiválasztásával és a gradiensek pontos meghatározásával a műszer környezetében. Megfelelő helyszín kiválasztásával biztosítható a környezeti hőmérséklet stabilitása és csökkenthetők az elsősorban forgalom okozta talajrezgések is. Ezek szem előtt tartásával választottuk a KFKI területén a Jánossy Földalatti Fizikai Laboratórium 30 m-es
mélységben lévő folyosóját. Méréseink szerint a helyszín hőmérsékleti stabilitása megfelelő, a napi változás mindössze néhány század fok, a mikroszeizmikus talajnyugtalanságot pedig az Eötvös-inga mellett elhelyezett nagy érzékenységű szeizmográffal tudjuk folyamatosan regisztrálni és korrekcióba venni.
A mérések legjelentősebb és legveszélyesebb hibaforrása a műszert kezelő és leolvasó személy jelenléte, elsősorban tömeghatása, ami a rendkívül érzékeny ingaszerkezet nyugalmi helyzetét megváltoztatja. Ugyanakkor az észlelő személy jelenlétével a műszer környezetében a hőmérsékleti egyensúlyt is megbontja és mozgásával egyértelműen érzékelhető talajrezgéseket kelt. A hibaforrás a közvetlen emberi jelenlét kiküszöbölésével, a mérési folyamat teljes automatizálásával, távvezérelt méréssel szüntethető meg.

A Pekár-inga vizuális leolvasásra szolgáló okulárjának helyére a 6. ábrán látható CCD érzékelőt szerelve az inga karjának nyugalmi helyzetét a keletkezett digitális kép kiértékelésével tudjuk meghatározni. Az általunk fejlesztett számítógépes képkiértékelési eljárással egy képpont tört részének megfelelő helyzet is meghatározható, így a leolvasási pontosság egy képről nagyjából 1/100 skálaosztás (az eredeti vizuális leolvasás esetén ez csak 1 skálaosztás, a tizedet már csak becsülni lehetett). Ha ehhez hozzávesszük, hogy az inga egyensúlyi helyzetéről nem csupán egyetlen leolvasást tudunk készíteni, hanem hosszabb időn keresztül másodpercenkénti több képet készítve maga a csillapodási görbe is meghatározható, akkor ez további jelentős pontosságnövekedést eredményez. Fejlesztéseinknek köszönhetően közel két nagyságrenddel jobb leolvasási pontosságot tudunk elérni, mint az eredeti vizuális észleléssel.
A mechatronikai megoldások közül a legkritikusabb elem az inga számítógéppel távvezérelt forgatását végző egység elkészítése volt. A forgatómotor vezérlését úgy kellett megoldani, hogy az inga különböző irányokba forgatása pontosan, üzembiztosan, ugyanakkor hirtelen gyorsulások és lassulások nélkül, a rendkívül érzékeny ingaszerkezet szempontjából kíméletesen, mechanikai sokkhatás nélkül történjen. Az inga különböző mérési irányokba forgatásához a 6. ábrán látható szerkezetet készítettük, a forgatásról speciális motor gondoskodik, az inga szabadon futó felső részéhez kapcsolódó bordásszíjas hajtáson keresztül [3]. A legtöbb alkatrész 3D nyomtatással készült. A Renishaw optikai enkódergyűrű alkalmazásával az ingaszerkezet különböző irányokba forgatott pozíciójának kiolvasási pontossága szögmásodperc pontossággal lehetséges.
Az átalakított műszerrel hosszan tartó és alapos tesztméréseket és kalibrációs méréseket követően a tényleges új ekvivalencia-mérések 2019. május 14.-én kezdődtek a földalatti laboratóriumban. A 7. ábrán az átalakított Eötvös–Pekár-ingát láthatjuk. A méréseket eddig arany, sárgaréz és alumínium próbatömegekkel végeztük sok hasznos tapasztalatot gyűjtve a további vizsgálatokhoz. Az adatok előzetes kiértékelése alapján Eötvösék eredeti mérési pontosságát már egy nagyságrenddel felülmúlva 10-10 pontossággal tudjuk igazolni az ekvivalencia-elv érvényességét arany, réz és alumínium tömegek esetére. Méréseinket további más anyagok vizsgálatára is kiterjesztjük, a végleges eredmények több éves további kísérletek után várhatók.

Az EPF-kísérlet megismétlése nem csak az említett szisztematikus hibára vonatkozó feltevésünket igazolhatja, hanem új szempontokkal járulhat hozzá a jelenlegi legpontosabb földi mérésekhez. Einstein általános relativitáselmélete eddig minden próbát kiállt, de a nagyon kicsi vagy nagyon nagy távolságokra vonatkozó inverz négyzetes távolságfüggés-tesztek, esetleg az ekvivalencia-elv mérések eredményei felvethetik a teljes érvényességi körének korlátosságát.
A mérésekben és ezek előkészületeiben az MTA Wigner Fizikai Kutatóközpontja, a Budapesti Műszaki és Gazdaságtudományi Egyetem Általános- és Felsőgeodézia Tanszéke, Irányítástechnika és Informatika Tanszéke és az Energetikai Gépek és Rendszerek Tanszéke, valamint az Egyesület a Tudomány és a Technológia Egységéért kutatói és mérnökei vesznek részt más további szervezetek, tanszékek és szakértők bevonásával. A kutatócsapat tagjai: Ván Péter, Barnaföldi Gergely, Deák László, Fenyvesi Edit, Lévai Péter, Somlai László fizikusok, Völgyesi Lajos geofizikus, Tóth Gyula és Égető Csaba geodétamérnökök, Kiss Bálint, Harangozó Péter, Péter Gábor villamosmérnökök, Gróf Gyula gépészmérnök és Szondy György villamosmérnök, független kutató.
VÖLGYESI LAJOS
IRODALOM
Nyitóképünk: Ingák Eötvös eredeti publikációjából [1]
[1] Eötvös R., Pekár D., Fekete E. (1922): Beiträge zum Gesetze der Proportionalität von Trägheit und Gravität, Annalen d. Physik, 11-66.
[2] Völgyesi L., Szondy Gy., Tóth Gy., Péter G., Kiss B., Deák L., Égető Cs., Fenyvesi E., Gróf Gy., Ván P. (2018): Előkészületek az Eötvös-kísérlet újramérésére. Magyar Geofizika, 59/4, 165-179.
[3] Péter G., Deák L., Gróf Gy., Kiss B., Szondy Gy., Tóth Gy., Ván P., Völgyesi L. (2018): Az Eötvös-Pekár-Fekete ekvivalencia-elv mérések megismétlése, Fizikai Szemle, 69/4, 111-116.
[4] Fischbach E., Sudarsky D., Szafe A., Talmadge C., Aronson S. H. (1986): Reanalysis of the Eötvös experiment, Physical Review Letters, 56(11), 3.
[5] Tóth Gy. (2019): Az Eötvös-Pekár-Fekete ekvivalencia-mérések szabályos hibája. Fizikai Szemle, 69/5, 155-188.
A cikk a Természet Világa 2019. novemberi számában (150. évf. 11. sz.) jelent meg.


