Tavaly volt 250 éve, hogy a Vénusz bolygó Nap előtti áthaladását Hell Miksa és Sajnovics János a sarkkörön túl, az észak-norvégiai Vardø szigetén figyelte meg. Útjuk egyike volt azon nemzetközi összefogással indított expedícióknak, amelyek a Nap távolságának megmérése céljából utaztak egymástól minél távolabbra. Az idén májusban 300 éve született Hell Miksa kitűnő matematikai és csillagászati készségével nemcsak az expedíció vezetésében, hanem a Nap távolságának megmérésében is nemzetközileg kiemelkedő szerepet töltött be.
A Csillagászati Egység (AU) a mai napig a csillagászat egyik legfontosabb alapegysége, amely a Nap-Föld közepes távolságával egyenlő. Gyakran alkalmazzák számításokhoz a Nap parallaxisát is, amely nem más, mint az a szög, amely alatt a Nap középpontjából 1 AU távolságban a Föld sugarának nagysága látszik, de mondhatjuk azt is, hogy a Nap egyenlítői horizontális parallaxisa. A Nap-parallaxis hivatalosan elfogadott értéke π = 8,79414”, így 1 AU = 149 597 870,7 km. A távolság direkt megmérésénél sokáig könnyebb feladatnak számított a napparallaxis meghatározása, ebből ez az alapvető távolságérték gyorsan kiszámolható.
A Nap nagyon kicsi parallaxisának meghatározása központi csillagunk vizsgálatával nehéz. A XVII-XVIII. században jó megoldást nyújtott a Földet megközelítő nagybolygók parallaxisának elegendően távoli két pontból történő közvetlen mérése, ennek nyomán a Kepler-törvények ismeretében a π kifejezhető. E célra időnként a Földet legjobban megközelítő Vénusz, illetve a valamelyest távolabbi földközelséget elérő Mars volt a legalkalmasabb, a földközeli kisbolygókat ekkor még nem ismerték.
A Vénusz legkisebb távolságát a Nap irányában éri el, mérésre a ritkán előforduló Napkorong előtti áthaladásai alkalmasak (1. ábra). E Vénusz-átvonulások furcsa törvényszerűséget követnek, nagyrészt párosával fordulnak elő, amelyeket 8 év választ el egymástól, azonban e párosok között legalább 105,5, de többször inkább 121,5 év telik el. Ritka esetben a 8 éves páros egyik tagja nem következik be, ekkor 113,5 év telhet el két átvonulás között.
A Vénusz átvonulását először 1639-ben figyelték meg, ennek során az angol J. Horrocks egy olyan téves elméletet követve, hogy a Napból nézve minden bolygó látszó átmérője azonos, kivéve a Marsot, a hibás Vénusz látszó szögátmérővel végzett számítások alapján a napparallaxisra 14” értéket kapott. A XVII. század közepén C. Huyghens foglalkozott a Naptávolság kérdéssel. Azon téves felvetése, hogy a Föld mérete a Vénusz és a Mars méretének átlaga, valamint műszeres méréseinek hibái úgy lerontották egymást, hogy 8,2” körüli értéket számolt. A Mars parallaxisának Franciaország és Cayenne távolságon végzett műszeres méréséből 1672-ben D. G. Cassini és J. Richter 9,5” körüli eredményt kapott. Érdekesség, hogy a francia N. L. Lacaille és J. Lalande közös 1751-es Mars megfigyelése nyomán az eredmény rosszabb, 10,4” lett, itt Lacaille a Jóreménység fokról észlelt.
1663-ban J. Gregory skót matematikus és csillagász világított rá, hogy a Nap előtt átvonuló Vénusz korábbiaknál pontosabb parallaxismérésre adhat lehetőséget. Ezzel egybevágó módszert javasolt E. Halley 1691- es, majd 1716-os munkájában, amelyek a tudományos érdeklődés fókuszába helyezték ez utóbbi csillagászt és az 1761/1769-ben esedékes Vénusz-átvonulás páros lehetőségét. A Halley-féle módszer után 1753-ban J. N. Delisle is ismertetett egy módszert, amely ugyancsak a Vénusz-átvonulásokat felhasználva, de egy másik, egyszerűbbnek tűnő számítási eljárással nyújt parallaxis mérési lehetőséget. Delisle azt is javasolta, hogy az 1761-es átvonulásnál a nemzetközi tudományos közösség koordinálja megfigyelő expedíciók munkáját a sikeres parallaxisméréshez.
Halley és Delisle módszere
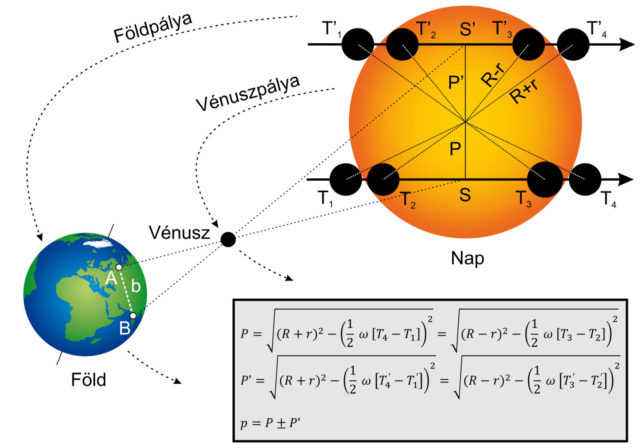
Halley módszere arra alapoz, hogy a Földön észak-dél irányban két jól megválasztott, egymástól távoli pontból történő Vénusz-átvonulás megfigyelés során a jelenség időtartama az észlelők számára eltérő. Az időeltérés abból adódik, hogy a Vénusz a Nap korongja előtt egyenletes szögsebességgel látszólag egy húr mentén halad végig, viszont a két megfigyelő által látott húrok a parallaktikus elmozdulás miatt különböző hosszúságúak lesznek. A Halley-módszer szerint a megfigyelőknek úgy kell elhelyezkedni, hogy azok a teljes jelenséget meg tudják figyelni, azonban az egyik a legrövidebb a másik a leghosszabb ideig látható átvonulást (és húrt) észlelje; majd ez alapján a két húr távolságát kell meghatározni.
Halley elméletét a első ábrán vázoltuk. A Föld felszínén az A és B megfigyelő az átvonulást S és S’ húrok mentén látja. A megfigyelők megmérik a külső és belső kontaktusok időpontjait, amelyek T1, T2, T3 és T4, illetve T1’, T2’, T3’ és T4’, majd ismerve a Vénusz relatív szögsebességét (ω≈4”/min) az egyes húrok hossza kiszámolható. Ismerve a Nap (R) és a Vénusz (r) látszó sugarának szögértékét a P és P’ szakasz, majd a p parallaxis kiszámolható. A p a két égitest közös parallaxisa, ismerve a megfigyelők egymástól való b távolságát és az égitestek távolságának arányait a π napparallaxis és az AU értéke már kifejezhető. A valóságban a két húr legnagyobb távolsága is valamelyest kevesebb, mint a Nap látszó szögátmérőjének 40-ed része, ez még a Vénusz látszó szögátmérőjénél is csekélyebb.
Az időmérés pontatlanságából eredő hiba abszolút értéke átvonulások és megfigyelők pozíciója szerint változó. Az 1769-es átvonulás során például, ha a földátmérő két végén – tehát a legideálisabb pozícióban – álló megfigyelők összesen 10 s időmérési hibát követnek el, az a napparallaxist körülbelül 0,9 százalékkal változtatja meg, nagyon durva 1 perces tévedés pedig több, mint 5 százalékos változást hoz létre. Könnyű belátni, hogy másodpercnyi tévedés is akár százezer kilométer nagyságrendű hibát jelenthet az AU értékben. A módszer számára legideálisabb és legkevésbé hibaérzékeny átvonulások azok, amelyek a Nap peremének északi vagy déli részéhez közel történnek, ugyanis a perem jelentősebb görbülete miatt a két megfigyelő sokkal nagyobb időkülönbséget (akár több, mint 1 órát is) mérhet. Közel centrális átvonulások esetén viszont inkább a Delisle módszerének használata javasolt.
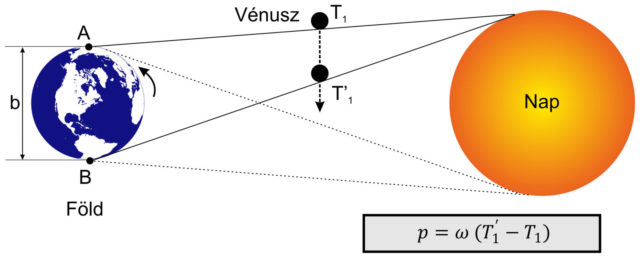
Delisle módszere a felhasználható észlelések számát növeli meg azzal, hogy egy megfigyelőnek elegendő akár csak egy kontaktus pontos időpontját észlelni. A módszer azt veszi figyelembe, hogy az átvonulás síkjában elegendően távol elhelyezkedő két megfigyelő a Vénusz-átvonulás adott kontaktusait más-más időpontban látja bekövetkezni. Nyilvánvaló, hogy így azok a helyek is mérésre alkalmasak, ahol csak a jelenség elejét vagy végét lehet megfigyelni és az időjárás változása is kevesebb kockázatot jelent.
A Delisle-módszer vázlata a 2. ábrán látható. Két megfigyelő áll az átvonulás síkjában a Föld két szélső pontján. Az A megfigyelő, aki számára a Nap éppen lenyugvóban van, a Vénusz belépését a Nap elé jóval előbb, T1 időpontban látja, mint a Föld bármely más részén álló megfigyelő. Belátható az is, hogy a B megfigyelő látja utoljára a Vénusz belépését a T1’ időpontban, számára pedig éppen akkor kel a Nap. Az azonos kontaktushoz tartozó mért időadatok és az ω ismeretében a p közös parallaxis szög gyorsan kiszámolható, majd a b távolság ismeretében a π is kifejezhető. Ha A és B megfigyelő a Föld két szélső pontjában van, akkor a kontaktusok között számukra körülbelül 11,5 perc eltérés mutatkozik. Minél közelebb vannak egymáshoz, annál kisebb ez az időkülönbség.
Mindkét módszernél igaz, hogy minél nagyobb a b távolság, a p értékben előforduló pontatlanság annál kisebb arányban megy át a π értékébe, a hiba akár ötödére is redukálódhat. Általában úgy tartják, hogy a Delisle-módszerrel – bár sokkal gyorsabb eljárás – az időmérés során elkövetett hibák nagyobb arányban jelentkeznek a parallaxisban, mint a Halley-módszer esetén. Ez a kijelentés az átvonulások nagyobb részére igaz, a már példának hozott 1769-es átvonulás során a földátmérő két végén álló megfigyelő számára a Delisle-módszer időmérési hibaérzékenysége meghaladja Halley-módszer érzékenységének 1,6-szorosát. Hozzá kell azonban tenni, hogy a Nap középpontjához közelebbi átvonulások során pont a Delisle-módszer válik az időmérés hibáira kevésbé érzékennyé.
Hell Miksa és az északi Vénusz
Tavaly júniusban volt 250 éve, hogy Hell Miksa és Sajnovics János az észak-norvégiai Vardø szigeten figyelte meg a Vénusz átvonulását a Nap előtt. Ez az expedíció is a minél pontosabb parallaxis mérést szolgálta, egyike volt azon nemzetközi expedícióknak, amelyek e célból egymástól minél távolabbi pontokra utaztak a jelenség megfigyelésére. 1769-ben a legdélebbi észlelést James Cook Tahitire vezető expedíciója szolgáltatta, a Hell-féle expedíció pedig a legészakibb észlelőhelyek egyike volt. Hell szakmailag is nagyon felkészültnek bizonyult az 1769-es átvonulás minél precízebb megfigyelésére, sokoldalú – nemcsak csillagászati – kutatási tervvel érkezett a szigetre.
Hell az 1761-es átvonulás megfigyelésének saját és nemzetközi eredményeit kielemezve rengeteg hibalehetőséget feltárt. Többek között ő is felismerte, hogy az addig elfogadott értéknél a Vénusz látszó szögátmérője kisebb, az égitestet fénylő gyűrű veheti körül és a két belső kontaktus esetén megjelenik egy „fekete csepp” nevű optikai jelenség, amely jelentősen korlátozza a kontaktusok mérését (3. ábra). Ez utóbbi miatt az időpontok mérési hibája több másodperc is lehet, pedig gyakorlatilag pont a belső kontaktusok lennének a pontosabban mérhetőek. Hell a megismert új adatok nyomán pontosította az 1769-es átvonulás adatait, a Vénusz pályaelemeit és az észlelés technikáját, ennek nyomán került a nemzetközi érdeklődés és a dán udvar figyelmébe az északi expedíció kapcsán. Mivel a jelenség idején Európában éjszaka volt, ezért csak a kontinens sarkkörön túli területeiről lehetett észlelni a jelenséget.
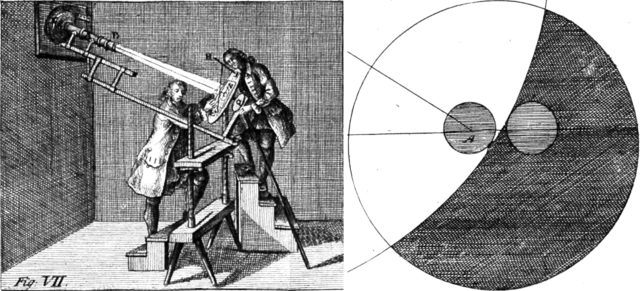
Az expedíció érkezése után a tudósok felépítették az obszervatóriumot a szigeten és nekiláttak a több hónapos felkészülésnek. Az expedíciónak nagy szerencséje volt a szeszélyes június eleji vardø-i időjárással, mivel pont a be- és kilépés idején bújt elő a Nap a felhők mögül. A jelenséget három távcsővel Hell, Sajnovics és egy Borchgrevink nevű diák észlelte, aki Trondheimben csatlakozott a kutatóexpedícióhoz, helyismereti és adminisztrációs segítség mellett az átvonulás észlelésbe is besegített. A távcsöves megfigyeléshez valószínűleg korommal bevont hosszúkás üveglemezeket alkalmaztak, ezek egyik végénél csekély volt a bevonat a másik végénél pedig vastag, szinte átláthatatlan, így az észlelés során mindig az éppen szükséges elnyelő részt tudták alkalmazni.
Az óra mellett segítők foglaltak helyet, akik részletesen közöltek minden időpontot az egyes észlelők jelzései szerint, ezek pedig jegyzőkönyvbe kerültek. Olyan időpontok is feljegyzésre kerültek, amikor épp még nem látni a kontaktus bekövetkeztét, vagy már éppen megtörtént, illetve a fekete csepp jelenség megjelenése, eltűnése. Az információk sokban segítettek Hellnek a lehetséges valós időpontok behatárolásában, javításában. Hell a külső érintés észlelését – értelemszerűen – nem tartotta kiemelten fontosnak, inkább a belső érintések pontos észlelésére koncentráltak.
A csillagászok az átvonulás után néhány órával, június 4-én, a földrajzi koordináták pontosítása miatt még egy napfogyatkozást is megfigyeltek, amely totalitási sávja Grönlandtól Északkelet-Szibéria felé haladt, Vardø-ből pedig egy jelentős takarású részleges fogyatkozásként látszott. Az átvonulási időmérések korrekciója és feldolgozása, majd Koppenhágában a Dán Királyi Tudományos Akadémia előtt 1769 késő őszén az expedíció tudományos eredményeinek ismertetése után, a többi mérés adatainak beérkezését követően Hell nekilátott a parallaxis meghatározásának.
Elmélet és gyakorlat
A XVIII. századi tudományos irodalmakra – talán nyomdatechnikai okokból is – jellemző módon a parallaxis számításáról sem állt rendelkezésre matematikai képletekkel történő levezetés. Például Halley is saját módszeréről csak egy szöveges leírást közölt. Lényegében a parallaxisszámítás gyakorlati, matematikai megoldása az alkalmazó kutató kreativitására volt bízva. A XIX. században néhány csillagászati szakkönyvben a Halley- és Delisle-módszer képletek formájában történő megoldására már lehetett találni fejezeteket, a 2004-es Vénusz-átvonulás előtti években pedig számos különféle pontosságú és bonyolultságú levezetés, tanulmány jelent meg, ezek bőven fellelhetők voltak az interneten is.
A Halley- és Delisle-módszer alkalmazásánál is azonos az elvárás: a megfigyelők tartózkodjanak e módszerek szerint elméletileg elvárt ideális észlelési pontokban, egymástól minél távolabb. Ez az expedíciók pontos megtervezését igényelte, amely során nyilvánvaló volt, hogy az ideális pontokról való észlelés sokszor korlátozott azok nehéz megközelíthetősége és egyéb okok miatt, így az ideálishoz minél közelebbi helyek elérésére kell törekedni.
A gyakorlatban a Delisle-módszer előnyeihez tartozik, hogy a Föld forgása nem igazán bonyolítja a számítást. Viszont, tipikus probléma a módszernél, ha megfigyelők az átvonulási sík helyett attól északra vagy délre helyezkednek el. A 4a. ábra példáján a kilépés belső érintését észlelni kívánó két megfigyelő az átvonulási síkban fekvő A és B ideális pontok helyett csak az A’ és B’ pontba tud eljutni. Ekkor a Nap peremének görbülete miatt T’A és T’B kontaktus időmérésből még akkor is hibás p érték kapható, ha az átvonulás síkjára vetített b távolságuk A és B-vel azonos marad. A B’ pontban álló megfigyelő által látott T’B időpont korábbi, mint a B pontban mérhető TB, mivel számára a Vénusz az SB ívet nem járja be. Az A’ pontban álló megfigyelő által mért T’A későbbi, mint az A pontból mérhető TA időpont, mivel a bolygónak a kilépéshez az SA ívet is be kell járnia. A helyes p érték számításához az SA és SB ívek okozta hibát a Delisle-módszer képletében korrigálni kell (4b. ábra). A számítást nehezíti, hogy a hiba nagysága is a keresett parallaxistól függ, további adatokra, mellékszámításokra is szükség van. E Nap pereme nyomán létrejövő hiba mértéke abban az esetben a legcsekélyebb, ha az átvonulás közel centrális.
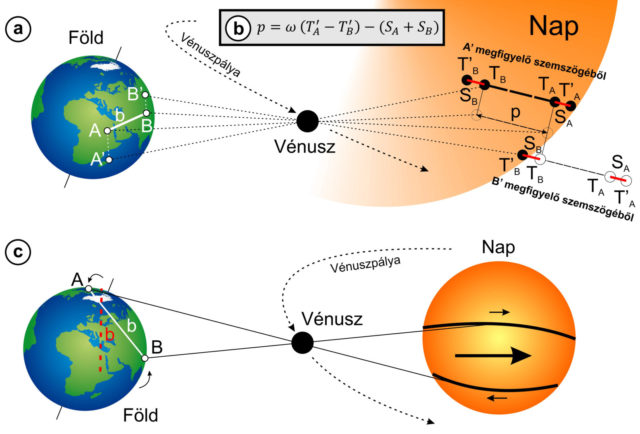
A klasszikus Halley-módszer elmélete esetén tipikus probléma a Föld forgása. Az a megfigyelő, aki az éjféli Nap előtt figyeli a jelenséget (mint 1769-ben Hell Miksa expedíciója), az mérséklődést, aki pedig a delelés közben, az enyhe növekedést észlelhet a Vénusz látszó szögsebességében (ezeket az ábrán kis nyilakkal jeleztük a nagy nyíllal jelzett átvonulási irány mellett). Ráadásul a forgás miatt a Vénusz útja a Nap korongja előtt a Föld felszínén álló A és B megfigyelő számára nem geometriai húr, hanem egy kis görbültségű ív. Tovább bonyolítja a problémát az átvonulási húrokhoz rendelhető bázistávolság meghatározása, mivel a Föld a nagy időkülönbség miatt jelentősen elfordul. Az említett problémákat bemutató 4c. ábrán piros szaggatott vonallal jelöltük azt a bázisvonalat, amely az A és B megfigyelőt kötötte össze az átvonulás kezdetekor. A Halley-módszernél nehéz a megfigyelőhelyeket az átvonulás síkjára ideális merőleges mentén a teljes átvonulás alatt kijelölni, így a korrekciós számítások itt sem mellőzhetőek.
A többször említett átvonulás síkjának (és koordinátarendszerének) felvétele – amely már az expedíciók és parallaxisszámítás tervezéséhez is fontos dolog – külön számítást igényel. A földi megfigyelő számára a Vénusz átvonulása során látszólag a Nap-Föld pályasíkhoz képest egy nagyjából 8 fokos dőlésű sík mentén a Nappal ellentétes irányban mozog, a két égitest mozgásából képezett sík közelíti legjobban az átvonulás síkját.
Az átvonulást jellemző és a számítási módszerekhez fontos két egymásra merőleges koordináta tengelytől való távolság miatt létrejövő parallaxis eltérést és ennek Föld forgása okozta megváltozását a tervezett megfigyelőhelyek szerint – korábbi számítások alapján feltételezett – parallaxis segítségével valószínűleg előre kiszámolták. A borítólap harmadik oldalán látható 1769-es expedíciók tervezéséhez készült anyag szövege és ábrázolása is kitér három példának hozott helyszín – Vardø, London, St. Cruz szigetek – parallaktikus eltérésére a be- és kilépés során, amely a későbbi parallaxisszámításhoz szükséges korrekciók nagyságáról is információval szolgál. A nagyon precíz számításnál elsősorban a Föld- és Vénusz- pályák ellipszis alakját kell még figyelembe venni és olyan tényezők is számításba jöhetnek, mint a Föld alakjának egyenlőtlenségei vagy a légköri fénytörés.
Hell Miksa és a napparallaxis
Hell vardø-i időmérése és az expedíció eredményei először 1770-ben jelentek meg nyomtatásban, saját parallaxisszámítás eredményei pedig először 1772-ben láttak napvilágot. Számításához négy állomás adatait használta fel: Hudson-öböl, Kalifornia, Tahiti és saját vardø-i mérése. A kiváló matematikai érzékkel rendelkező Hell is valószínűleg tisztában lehetett a számítás gyakorlati problémáival, viszont a parallaxist közlő publikációban nem nevezi meg a számítási módszert. A kiadvány – a korra jellemzően – matematikai levezetést sem tartalmaz, így csak következtethetünk a használt eljárásra. Számításai alapján a Nap parallaxisát 8,70” értékben határozza meg.
Feltételezhető, hogy a Halley- és Delisle-módszert a vizsgálat alá vett észlelési párok elhelyezkedése szerint felváltva használta. Az Észak-amerikai adatok és saját vardø-i adatainak összevetése esetén nagy valószínűséggel a Delisle-módszert használta, a helyszínek a módszer alkalmazásához kedvezően helyezkedtek el. Tahiti és Vardø összevetése esetén feltételezhető, hogy a Halley-módszert választotta, e két helyszín pozíciója is ezt indokolná.
Viszont az is valószínűsíthető, hogy Hell a saját számításának és a parallaxis legvalószínűbb értékének ellenőrzése céljából egy saját, fokozatosan közelítő módszert is kigondolt, amely úgy tűnik nemzetközi viszonylatban is először alkalmazott eljárás lehetett.
Először felvett egy korábbi számítások alapján becsült kezdő parallaxis értéket, ebből az egyes megfigyelőhelyekre kiszámolta a kontaktusok időpontjait. A megfigyelőhelyeken mért adatok és a számolt adatok közti eltérés nyomán pontosította a parallaxist, majd ebből újra kontaktus időpontokat számolt. Az eljárást ismételve, fokozatos közelítéssel addig finomította a parallaxist, amíg minden állomás méréséhez viszonyítva a legkisebb időpont eltéréseket (mérési hibát) kapta. A módszer már magában hordozta annak a „legkisebb négyzetek módszerének” a csíráját, amelyet Gauss pár évtizeddel később írt le.
A kontaktusok időpontjának számítása igazából egy gyorsabb és kevésbé bonyolult eljárás. Ilyenkor az adott kontaktushoz meghatározzák, hogy az a Föld középpontjából milyen időpontban lenne látható, majd a parallaxis érték ismeretében ezt korrigálják a megfigyelő helyzete alapján, a helyszínen várható időpontra.
Nem zárható ki, hogy Hell a módszere ötletét egy 1769. júniusi londoni újságcikk nyomán gondolta ki. A vardø-i expedícióról részletes naplót író Sajnovics János közöl a napló mellékletében egy újságidézetet, amelyben Londonra vonatkozóan a csillagászok 4”-10” között 0,5” lépésekkel az egyes parallaxis értékekhez meghatározták a belépés idejét (Angliából csak a jelenség eleje látszott), erről egy táblázat is készült. Viszont a módszerrel csak annyit sikerült meghatározniuk, hogy a parallaxis érték sokkal kisebb, mint ahogy azt
gondolták. A gyakorlatban ez a módszer akkor alkalmazható, ha a Nap-Vénusz páros zenittávolsága, így horizontális parallaxisa nagy (ez London esetén fennállt), viszont egyetlen állomás esetén megbízhatatlan eredményt ad.
Összességében elmondható, hogy a parallaxisszámításhoz 1769-ben több megfigyelés is az egyes módszerek tekintetében kedvező helyen történt, természetesen nem feledhetjük azt sem, hogy egyes expedíciók évekig tartottak csak egyetlen megfigyelés céljából, amit sokszor a rossz időjárás hiúsított meg. Hell 8,70”-es eredménye nem a legpontosabb érték! A francia A. G. Pingré 8,80”-es értéke szinte majdnem pontos, az oxfordi matematika professzor T. Hornsby, a Hell mérését is felhasználó 8,78”-es értéke szintén jól közelíti a napparallaxis valós értékét.
1769 után
A XVIII. századi Vénusz-átvonulások nem hozták meg a várt pontosságot. A jelentősebb számítások π értékei 8,43-8,84” között szóródtak, így annyit lehetett csak megállapítani, hogy a valós érték valahol ezek között foglal helyet. Hell parallaxis eredménye ezek átlagába esett bele, azonban a tudományos közösségben tekintélynek számító Lalande 8,50”-es értéke vált elfogadottá, miután a francia és szentpétervári akadémiák tekintélye nyomán több számoló is inkább elvetette saját, sokszor pontosabb eredményét. Hell azonban kitartott saját számítása helyessége mellett, e magabiztosságra utalhat talán az is, hogy Sajnovics János 1778-as Idea Astronomiae című könyvében a Hell-féle eredmény alapján mutatja be német mérföldben az egyes ismert égitestek távolságát.
Talán pont saját tekintélyének védelme volt az egyik oka, hogy Lalande megkérdőjelezte a Hell-féle mérés valódiságát és az adatok hibáira akart rámutatni. Lalande minél több állomás adatát be kívánta vonni számításába, ezért sérelmezte, hogy Hell késlekedik mérési adatai közzétételével. Még az a vád is felmerült, hogy nem látta az átvonulást, de ha látta is nagyon rosszul mért és egy finn állomás adatait kombinálta át. A vád alaptalan volt. Lalande nem tudhatta, hogy Hellnek először a Dán Királyi Tudományos Akadémia előtt kellett beszámolnia adatairól, csupán azt követően tehette közzé. A vita tudományos értekezések és bizonyítások formájában elegánsan és megnyugtatóan lezárult, Lalande később már kifejezetten elismerően nyilatkozott Hellről és eredményeiről, e méltatás későbbi munkáiban is megjelenik. A Lalande-féle hibás számítás háttere az is lehet, hogy az adatsorban több hibás koordinátájú helyszín is szerepel, olyan is, amit Hell például pont ezért kihagyott a végső számításból.
Pár évtizeddel később, 1835-ben egy fiatal bécsi csillagász, K. L. Littrow szintén az adatok megmásításával vádolta meg Hellt, kézirataiban kivakarást és más szívű tintával történő javításokat, átírásokat vélt látni. A támadás háttere összetett, talán az is közrejátszott, hogy az általa nagyon tisztelt J. F. Encke átvonulás-adatokból újraszámolt hibás 8,57”-es értéke védelmében lépett fel. Vádjai viszont egészen az évszázad végéig rossz színben tüntették fel Hellt. S. Newcomb a XIX. század végének jelentős amerikai égi mechanikusa tisztázta a kérdést, miután 1883-ban Bécsben Hell eredeti kéziratait tanulmányozta. A rendkívüli precizitással eljáró Newcomb még olyan kísérleteket is elvégzett, hogy a kéziratok egy viszonylag üresebb lapján kivakarást vagy különböző átírásokat alkalmazott és összevetette Hell írásával. Egyértelművé vált, hogy Hell az adatokban semmi módosítást nem tett, ezeket a különböző színű átírásokat az amúgy színtévesztő Littrow nem is vehette volna észre.
A XIX. század első kétharmadában a Vénusz-átvonulások adataiból több újraszámítás is történt, de a parallaxis értéke így sem lett 8,53”-8,57” közötti értéknél több. A XVIII. századi mérések pontatlansága a mérési technikával és a hibás észlelési koordinátákkal is magyarázható lenne, de a Vénusz-átvonulás nyomán számolt parallaxisértékek eredményeiben az 1874/1882-es jelenségpáros során a – sokszor fotografikus – észlelések sem javítottak jelentősen. A méréseket heliométer segítségével és Hansen-módszerrel értékelték ki, a Nap középpontjától adott időpontokban – valamint fényképsorozatok segítségével – megmért távolságok alapján az átvonulás húrja kirajzolható és a parallaxisszámítás is elvégezhető. A meghatározott parallaxisok 8,76-8,88” között mozogtak, a legalaposabb számítást Newcomb végezte el, aki 1883-ban 8,792” értéket adott meg. Nyilvánvalóvá vált, hogy a Vénusz-átvonulások módszerével a kellő pontosság elérése korlátozott, a parallaxis pontosságát a fotográfia és a távcsövek teljesítményének növelése sem javítja számottevően. Erre az eredményre jutott a mindkét jelenséget megfigyelő, fényképezés szakterületén is nagyon járatos csillagász, Weinek László is.
A 2004-ben esedékes Vénusz-átvonulás idején már elég széles körben rendelkezésre álló GPS, digitális kamerák és fényképezőgépek nyomán sokan azt várták, jósolták, hogy talán sikerül meghaladni a régi idők és technikák korlátait és pontosabb parallaxismérést lehet végezni. Az akkor már nagy pontossággal ismert parallaxis érték mellett inkább a kíváncsiság állt a kezdeményezések mögött. Az Európai Déli Obszervatórium (ESO) egy VT-2004 nevű programot hirdetett, ebbe minden motivált észlelő beküldhette saját észlelését, amelyből végül a francia IMCCE (Égimechanikai és Efemerisz-számoló Intézet) két munkatársa parallaxist számolt. Több ezer mérés érkezett be. Az adatot beküldő megfigyelők a projekt honlapja segítségével megfelelő észlelőpárt kiválasztva saját adataikra is végezhettek parallaxis számítást, ezen kívül fotók kiértékelésére is volt lehetőség az 1874/82-es átvonulások során alkalmazott módszerhez hasonlóan.A beérkezett adatok alapján az IMCCE kutatói a nyilvánvalóan hibás értékek eltávolítása és különféle szigorúsággal történt szűrések, összevetések, valamint statisztikai megoldások segítségével a – Hell által is alkalmazott – fokozatos közelítés módszere alapján π értékére 8,793511” értéket kaptak. Az észlelőpárok nélküli, „online” beküldő helyzetére előre jelzett és általa beküldött időpontokra legkisebb eltéréssel illeszkedő parallaxisok alapján 8,798158” érték adódott, amely az észlelő amatőrcsillagászok precíz munkáját dicséri (5. ábra). E két nagyon jó eredmény azonban, a mai pontos parallaxis ismeretében készült szigorú adatszűrés eredménye. Megfelelő adatok alkalmazásával és mérsékeltebb szűréssel számítást végeztek a Delisle-módszer alapján is, ekkor rosszabb, 8.779881” érték lett az eredmény. A Delisle-módszer eredménye a korábbi évszázadok számításait összevetve mégis figyelemre méltónak vehető, viszont az a következtetés is levonható, hogy az észlelések nagyobb száma nem növeli a pontosságot.
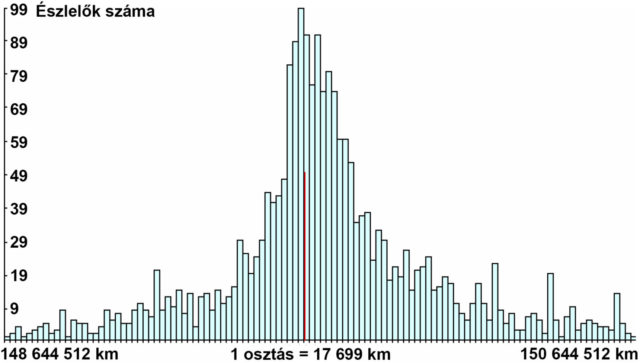
A 2012-es Vénusz-átvonulás során is történtek próbálkozások a parallaxis meghatározására, azonban nem egy nagy globális program égisze alatt, hanem több kezdeményezés is indult és különféle mennyiségű észlelések alapján készültek számítások. A digitális technika is sokat finomodott a 2010-es évekre, így talán valamelyest több lehetőség állt az megfigyelők rendelkezésére. Talán a jól megválasztott kevesebb számú észlelés is állhat annak hátterében, hogy az egyes projektek adataiból a legjobb átlagos parallaxis érték 8,783” lett a Delisle-módszer alkalmazásával. A legtöbb észlelést bevonó program átlagai nem eredményeztek sokkal jobb parallaxist, mint amit évszázadokkel előtte Encke vagy Lalande számolt! Érdekesség, hogy a 2012-es mérések kiértékelése során inkább a Delisle-módszer bizonyult pontosabbnak, erre talán valamelyest magyarázat lehet az is, hogy 1639 óta ez volt a Nap központjához legközelebbi átvonulás, amely e módszer használatának is kedvez.
Összeségében úgy tűnik, a digitális technika és képfeldolgozás ellenére a 2004/12-es átvonulások észlelései a parallaxis pontosságot nem növelték meg jelentősen, tehát a Vénusz-átvonulás módszer korlátait a XIX. században már sikerült elérni. Az Oxfordi Egyetem Tudománytörténeti Múzeuma a 2004-es Vénusz-átvonulás alkalmából a XVIII. századi brit részvétel történeti emlékeiből egy kiállítást rendezett, amely A legnemesebb probléma a természetben címet viselte. Talán nem is lehetne szebb névvel illetni e témakört. Hell Miksa ebben betöltött nemzetközi szakmai munkájának jelentősége pedig vitathatatlan.
Utószó
A szerző tisztelettel emlékezik Teres Ágoston csillagászra, aki Hell Miksa és Sajnovics János emlékét nagy gondoskodással ápolta. A szerző köszöni Bartha Lajos és Péntek Kálmán mindenkori segítségét a Vénusz-átvonulások és napparallaxis témakörérének tanulmányozása során.
MITRE ZOLTÁN
IRODALOM
[1] Abonyi, I. (2010): Hell Miksáról, aki 1769-ben elsőként mérte meg a Nap-Föld távolságot. Fizikai Szemle, LX. évf. 7–8. sz. pp. 243-252.
[2] Bartha, L. (1969): Hell Miksa expedíciója és a Csillagászati Egység kérdése. Csillagászati évkönyv 1969, Gondolat Könyvkiadó, Budapest, pp. 146-164.
[3] Bartha, L. (2004): Vénusz-átvonulások és magyar megfigyelőik. Gothard Amatőrcsillagászati Egyesület, Egyesületi Füzetek 3., pp. 6-29.
[4] Kövesligethy, R. (1899): Az égi testek távolságai. Parallaxis. A mathematikai és csillagászati földrajz kézikönyve. Kogutowicz és Társa Magyar Földrajzi Intézete, Budapest, pp. 381-397.
[5] Péntek, K. (2004): A Vénusz-átvonulásának matematikai leírása Halley-módszere alapján. Gothard Amatőrcsillagászati Egyesület, Egyesületi Füzetek 3., pp. 30-45.
[6] Tuboly, V.; Bartha, L.; Mire, Z.; Keszthelyi, S.; Mizser, A.; Szabó, S. (2004): A fekete Vénusz. Vénusz-átvonulások a Nap előtt. Hegyháti Csillagvizsgáló Alapítvány, Hegyhátsál, 169 p.
A cikk a Természet Világa 2020. májusi számában (151. évf. 5. sz.) jelent meg.


