A fizikát többféle módon lehet elméletekre osztani. Vannak kvantumos és klasszikus, relativisztikus és nemrelativisztikus elméletek, vagy akár az alapvető kölcsönhatások szerint a gravitáció, elektromágnesség, a gyenge és erős kölcsönhatások elméletei. Vannak továbbá a mezőelméletek, amelyekben az alapvető fizikai mennyiségek tér- és időfüggő, illetve téridőfüggő mezők, és vannak másféle elméletek is, például a klasszikus pontmechanika. Ezenkívül pedig ott van a termodinamika.
A klasszikus, azaz nemkvantumos és nemrelativisztikus fizika három nagy elmélete közül a legrégebbi a mechanika, a termodinamika korban talán a második. Vagy a harmadik, attól függ, hol zárjuk le az elektrodinamika és a termodinamika kialakulását, tehát például Maxwellnek vagy Fowlernek tulajdonítjuk a nulladik főtétel megfogalmazását, amelyik az időben utolsó főtétele a termodinamikának. Az biztos, hogy a termodinamika mindenképp fiatalabb, mint a mechanika. A mechanikát Newtontól számíthatjuk, a termodinamikát pedig Carnot-tól, száz év a különbség. A mechanika prototípusa a tökéletes mozgás, az égimechanika, a termodinamika pedig a hőerőgépek magyarázatára, a mérnöki tapasztalatok mechanikával nem megfogható részének leírására született, a világunk fizikai tökéletlenségének elméleteként. A második főtétel korai változatai szerint mindig van veszteség, soha nem lehet 100%-os hatásfokú gépet konstruálni és az elérhető legnagyobb hatásfok semmi mástól, csakis a környezettől, annak is csak a hőmérsékletétől függ. Mindegy milyen a gép anyaga és szerkezete, a maximális, azaz a Carnot-hatásfok nem függ ettől. Ebben az értelemben tehát nemcsak maximális, hanem egyúttal univerzális. Ez persze egy emberközpontú kép, egy természettörvény nem foglalkozik gépekkel, az univerzalitás általánosabban az anyag szerkezetétől való függetlenséget jelenti.
A fizika első nagy egyesítése
A második főtételt manapság a folyamatok egyfajta irányultságaként fogjuk fel, tudományosabban irreverzibilitásnak nevezzük. Jellemzője, egyfajta mértéke a disszipáció. Disszipáció mindenütt van, nemcsak a földi léptékű technológiában, a kvarkszinttől a galaxishalmaz-méretekig. Van relativisztikus termodinamika, kvantumos termodinamika, vannak termikus kvantumtérelméletek és a fekete lyukak hőmérsékletéről is szoktunk beszélni. A termodinamika elmélete és fogalmai a kémiában, a biológiában elkerülhetetlenek, de a közgazdaságtanban is kerülgetik őket. Ha a valóság nem ideális, akkor megfelelő eszközrendszer kell a megértéséhez. Ez pedig a termodinamika, messze túl a hőerőgépeken.
Két fontos kérdés merül fel itt. Az első, hogy vajon honnan ered az irreverzibilitás, a folyamatok irányultsága? A második, hogy pontosan mi az oka az univerzalitásnak, azaz a megfigyelt anyagfüggetlenségnek? Ha ez utóbbit megértjük, akkor kiderülhet, miért használható a termodinamika ilyen sok területen.
A fizika első nagy egyesítése elképzel egy választ ezekre a kérdésekre. A Boltzmann nevéhez köthető statisztikus mechanika besorolta a termodinamikát a mechanika alá. Ezek szerint a folyamatok irányítottságának oka a komplexitás, a sok összetevő, a termodinamika pedig emergens, származtatott elmélet, mélyebb szinten minden ideális és leírható a mechanika törvényeivel. Elképzelhető, hogy az univerzalitás is ebből származik, mindegy, miféle mechanizmusok, részecskék, mezők és kölcsönhatások alkotják a hőerőgépet, illetve az anyagot, az eredmény független lehet az összetevőktől. A zűrzavar, ami egyetemleges. Ráadásul a világ megnyugtatóan ideális marad, valahol mélyen, a mikroszkopikus szinten. Mint ahogy a bolygók és csillagok mozgása is a tökéletes mozgás mechanikai törvényeit követi.
A statisztikus fizika hatalmas és sikeres elmélet, de önmagában, pusztán mechanikából máig sem magyarázza a második főtételt. Mindig kiderült, hogy valahogy kell még egy extra hipotézis. A részecskék mozgását leíró tökéletesen ideális mechanikai mozgásegyenletek önmagukban nem elegendőek a makroszkopikus folyamatok irányultságának magyarázatára. Valamennyire persze igen, a leegyszerűsített anyagmodelljeink, mint a rugalmas golyók, tömegpontok, vagy oszcillátorok meglepően hatékonyak. De a speciális rendszerek csak akkor érdekesek, ha az univerzalitás érvényes. Ugyanis ekkor, és csak ekkor következtethetünk a speciális (különös) modell tulajdonságaiból általános dolgokra. Mint például ahogy ezt Planck tette a feketetest-sugárzás esetén. Ha nincs univerzalitás, akkor nagyon keveset tudunk meg a világból egy oszcillátorrendszer vizsgálatával. Tehát amit a statisztikus mechanikával megérthetünk a folyamatok irányultságából, az korántsem minden.
A termodinamika minden elméletében gondosan szétválasztjuk az univerzális és az anyagfüggő, azaz konstitutív fogalmakat. A hőmérséklet univerzális, de a fajhő nem az. Az univerzalitást bizonyító gyönyörű gondolatmenetek, például az abszolút hőmérsékletre vonatkozó, olyan egyszerű feltevéseket használnak, mint a folyamatok reverzibilitása, illetve az
állapothatározók létezése. Egyszerű, de egyáltalán nem triviális feltevéseket. A nulladik főtétel, amely a termodinamikai egyensúly tranzitivitását mondja ki a legismertebb formájában, tartalmilag a fizika redukcionista felfogásának alapja: a szeparálhatóságot posztulálja, azt, hogy a kölcsönhatások világában, ahol minden mindennel összefügg, értelme van egy fizikai rendszert az állapothatározóival, azaz önmagában jellemezni. Vannak saját jellemzői és azok elegendőek. Ez egy nagyon mély, és egyáltalán nem magától értetődő dolog, azért tartjuk magától értetődőnek, mert bele van kódolva a szavainkba: az én „állapotomat” meg tudom adni csak a saját magam megfigyelésével, a környezet az más, az különbözik tőlem. A világ részekre szedhető. Mindig így van ez? A termodinamikában megadjuk ennek explicit modellfeltételeit [1], és a termodinamikai egyensúly fogalmához kötjük.
Egyensúly és nemegyensúly
A termodinamikai egyensúly fogalmát minimum három különböző módon szokás érteni és keverni. Egyrészt időfüggetlenségként, de nem minden időfüggetlen rendszer egyensúlyi: az elektromos áram vagy a hő lehet független az időtől. Aztán homogenitásként, azaz térfüggetlenségként, de van egyensúlyban lévő inhomogén rendszer: a hőmérséklet változik a magassággal a barometrikus magasságformula szerint. Harmadrészt pedig, és ez talán a legpontosabb, az egyensúlyt a részecskerendszereink átlagos mennyiségekkel történő jellemezhetőségének is tartjuk: bizonyos speciális, termikus sebességeloszlással jellemezhető gázok ilyen értelemben tekinthetőek egyensúlyinak. Viszont nem világos, mely sebességeloszlás egyensúlyi (nem minden entrópia logaritmikus), és más oldalról sem elég ez a meghatározás. Hiszen vannak nem részecskeszerű mikro- és mezostruktúrák, amelyeket reménytelen és lehetetlen statisztikailag vizsgálni, de makroszkopikus szinten kielégítő modelleket kapunk termodinamikai leírással. Gondoljunk itt egy mikrorepedezett, mikrokristályos kődarabra.
Nemegyensúlyi termodinamikáról akkor beszélünk, ha az iménti három feltétel valamelyike sérül. Ennek megfelelően legalább három modellezési szintre oszthatjuk. A legegyszerűbb esetben csak az első feltétel sérül, egy homogén közegben idővel megváltoznak a termosztatikai állapothatározók. Például mérjük, hogy egy szobában a hőmérséklet hogyan változik. Ezt nevezhetjük közönséges, vagy időbeli termodinamikának. Leginkább a klasszikus technológiai folyamatok leírására használjuk, tipikusan ide tartozik a Newton-féle lehűlési törvény, egyik fontos felfedezése a Curzon-Ahlborn-hatásfok, amely szerint maximális teljesítményre optimalizált véges időtartamú Carnot-ciklusokkal működtetett hőerőgépeknek a hatásfoka képlet, ahol T1 és T2 a környezeti hőmérsékletek. Ez egy praktikus korlát, kisebb és kevésbé univerzális, mint a Carnot-hatásfok, képlet. Ez utóbbi elvileg csak „végtelen lassú” folyamatokkal megközelíthető.
A második fontos eset a klasszikus irreverzibilis termodinamika, amikor időben és térben változhatnak a fizikai mennyiségek, viszont azok ugyanazok, mint az egyensúlyi homogén rendszerekben mért állapothatározók. Ez a modellfeltevés, a lokális egyensúly hipotézise, azon alapul, hogy a kis fizikai rendszer hasonló a nagyhoz. Kidolgozását kezdte Onsager, folytatta Eckart és Prigogine többek között, a múlt század 40-es éveitől. Egységes rendszerbe foglalja a hővezetés, a diffúzió és a viszkózus áramlások modelljeit, kémiai és energetikai technológiáink lényegében ezen az elméleten alapulnak.
A harmadik ága a nemegyensúlyi termodinamikának a mindhárom értelemben nemegyensúlyi rendszereket vizsgálja, tehát a téridőben inhomogén komplex anyagokat, amelyek leírásához a mikroszerkezet termikus egyensúlyi eloszlásának paraméterei nem elegendőek. A legjobban felderített ilyen termodinamikai rendszer a ritka gázok, ahol a statisztikus mechanika nemegyensúlyi ága, a kinetikus gázelmélet és a nemegyensúlyi termodinamika közvetlenül érintkezik. A mikroszerkezetet a lehető legegyszerűbbnek feltételezve, töltetlen tömegpontok, vagy merev golyócskák ütközéseire vonatkozó részletes feltételekkel aránylag egyszerűen megkaphatjuk az átlagos mennyiségekre vonatkozó klasszikus irreverzibilis termodinamika Fourier- és Navier-Stokes-egyenleteit és ezeknek az általánosításait is, amit kiterjesztett termodinamikának nevezünk. Magyarországon ennek az elméletkörnek az úttörője Gyarmati István volt.
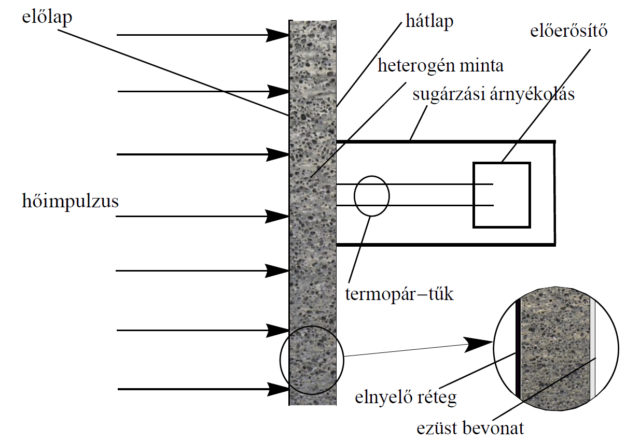
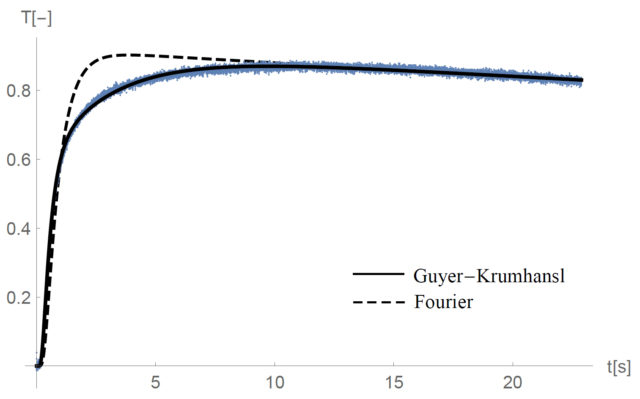
Mindhárom szinten rendelkezünk a folyamatok irányultságáról. A vonatkozó matematikai modelljeink az entrópia növekedését írják elő, ez pedig irányt mutat a folyamatoknak. Valóban észszerű következményei vannak, például, hogy a hő a melegebb helyről a hidegebb felé terjed. Ez a Fourier-törvény. A klasszikus irreverzibilis termodinamikában szokásos állapothatározók változására, mint a tömeg vagy az energia, adottak az egyenleteink: ezekre a mennyiségekre megmaradási tételek vonatkoznak. A megmaradási tételekre ad megszorításokat a második főtétel. A kiterjesztett termodinamikában azonban további állapothatározók is vannak, mint például a hőáramsűrűség, és ekkor új mozgásegyenletekre, helyesebben, mivel szó sincs mechanikáról, új fejlődési egyenletekre van szükség. Honnan vesszük ezeket az új fejlődési egyenleteket, például konkrétan a hőáram sűrűsége hogyan változik? Mi is ekkor a második főtétel? A ritka gázok esetén, ha nagyon egyszerű az anyag szerkezete, akkor ezt felhasználva levezethetőek a makroszkopikus, mérhető mennyiségekre vonatkozó fejlődési egyenletek. Bonyolultabb esetekben, mint például a fentebb említett kődarab, ilyesmi lehetetlen. Márpedig megmérhető, hogy egy kődarabban sem teljesül a Fourier-törvény, tehát valami jobb leírás kell (1-2. ábra). Ráadásul a kísérletek azt mutatják, hogy a Fourier-törvény ritka gázokra kitalált általánosítása, a Guyer-Krumhansl-egyenlet, jól leírja a hő megfigyelt, nem hagyományos terjedését egész más anyagokban, például kövekben is [2]. Ezzel itt konkrétan fülön csíptük a fent említett univerzalitást. De vajon miért működik ennyire hasonlóan a kő és a gáz?
Irreverzibilitás és stabilitás
Valójában a fenti kérdés egészen másként merült fel. Nem a kísérlethez kerestük az elméletet, hanem az elmélet alapján terveztük a kísérletet. A kő és a gáz hasonló viselkedése egyaránt a második főtétel következménye. Ez alapján a hő nem mindig a melegebb helyről a hidegebb felé terjed még tiszta hővezetés setén sem. Ennek ellenére ez a terjedési mód sem használható ki korlátlanul munka előállítására, továbbra is tiltott mindkétféle örökmozgó. Viszont ez a tiltás a konkrét esetben, azaz a hőáramsűrűségre, lehetővé teszi a megfelelő fejlődési egyenlet meghatározását, konkrétan az előbb említett Guyer-Krumhansl-egyenlet is levezethető a második főtétel alapján, szerkezeti feltevések nélkül.
De mit is jelent akkor a folyamatok irányítottsága, világunk működésének alapeleme, amelyet a termodinamika második főtételéhez szoktunk kötni? Hiszen eddig sem igazán tudtuk mitől nő, vagy micsoda is az entrópia, hát még a kiterjesztett entrópia. A nemegyensúlyi termodinamikában erre határozott és egyszerű választ kapunk.
Technikailag, logikailag látszólag bonyolódik a helyzet, mert a második főtétel összetett, több független részből áll. Egyrészt, először is itt van maga az entrópiafüggvény, mint a termodinamikai állapottér potenciálja, amely konkáv. Önmagában nincs maximuma (gondoljunk az ideális gázra, amelynek entrópiája a tömeg, a belső energia és a térfogat függvényeként, S(E,V,M) = M ln((E/M)C(V/M)R)), nincs maximuma. A konkávitása azt biztosítja, hogy kölcsönhatásban, tehát mondjuk bármely adott hőmérsékletű, nyomású és kémiai potenciálú környezettel együttesen maximuma legyen a gáz és a környezet teljes entrópiájának. Egyensúlyban. Másrészt pedig a folyamatokat meghatározó anyagi tulajdonságok olyanok, hogy ez a teljes entrópia növekszik, tart a környezet által meghatározott maximumához. Azaz például a hőátadási tényező, a tömeg, a viszkozitás stb. adott előjelű, és nem lehet más. Ez a sok különféle feltevés együttesen biztosítja a termodinamikai rendszerek egyensúlyának stabilitását. A meleg tea az asztalon lehűl, mert a fajhője pozitív (az entrópia konkáv), a hőátadási tényező pozitív (itt a hő melegebb helyről a hidegebb felé terjed). A második főtétel részei, az entrópia mint potenciál, a konkávitása és a növekedése független feltevések, részletes és egyenként kézzelfogható fizikai értelmezéssel.
Összességében pedig egy matematikai tétel feltételeivé állnak össze: az entrópia a termodinamikai egyensúly Ljapunov-függvénye. Az ezen alapuló elméletben a fejlődési egyenletek meghatározott egyensúlyai asszimptotikusan stabilak lesznek. Ez azt jelenti, hogy elmozdítva egyensúlyi helyzetükből visszatérnek oda. Ha kicsit felmelegítem a kávémat, megint ki fog hűlni. Ha nem lenne stabil, akkor ehelyett felrobbanna. De akkor nem is figyelhetném meg, legalábbis nem mint kávét [3].
A folyamatok megfigyelt irányultságának oka ez. Azok a fizikai elméletek, amelyek ezt a fajta stabilitást előírják, beépítik és ezt helyesen teszik, azok jól modellezik a természetben megfigyelt kiegyenlítődési folyamatokat, amelyek nem használják a második főtételt, azoknak ezeket a tulajdonságokat különböző más feltevésekkel és trükkökkel kell megmagyarázni. A termodinamikai egyensúly stabilitása a valóságnak egy olyan erős kvalitatív tulajdonsága, hogy önmagában felhasználható a vonatkozó matematikai modellek kiépítésére. A legegyszerűbb nemegyensúlyi termodinamikai elméletben, a közönséges termodinamikában ezt kiválóan leírta Matolcsi Tamás [4]. A nemegyensúlyi termodinamikában lehet tudni, hogy miért és mitől növekszik az entrópia.
Természetesen ez csak az általános helyzet, és a kivételek is roppant érdekesek: a fázisátalakulások, vagy a fekete lyukak mind termodinamikai instabilitásokkal kapcsolatosak. Azt gondolhatnánk, hogy ha jól ismerjük az anyag szerkezetét és a rá vonatkozó törvényeket, mozgásegyenleteket, akkor mindez felesleges, úgyis kijön, hiszen a termodinamika emergens. Azonban a stabilitási háttér negligálása számos esetben súlyos elméleti és ebből következő gyakorlati problémákra vezetett. Ez az oka annak, hogy a kinetikus elméletből a legegyszerűbb eseten túl nehéz használható gázegyenleteket konstruálni, a Navier–Stokes-egyenletek ilyen kiterjesztései (a Burnett-egyenletkör) instabilak. Ez az oka, hogy a kapillaritást leíró statikus anyagtörvényekkel (még a XIX. század, Van der Waals-tól) nem tudunk értelmes folyadékelméletet gyártani, a Korteweg-folyadékok megoldásai általában felrobbannak. Ez az oka annak is, hogy mostanáig sincs egyszerű elmélete a relativisztikus disszipatív folyadékoknak. A Navier–Stokes-egyenlet legegyszerűbb relativisztikus általánosítása alapján a víz instabilabb mint egy begyújtott atombomba. Femtoszkundumos a kiszámolható robbanási ideje akármilyen kis mennyiségben.
Gondolhatjuk persze, hogy mindez csak tudásunk hiánya, még egy kicsit át kell gondolnunk a feltételeket, esetleg másként átlagolni. Hiszen jól ismerjük a mikroszkopikus törvényeket. No de honnan is?
Fejlődési egyenletek: ideális vagy nem?
A fizika törvényeit, azaz a fizikai mennyiségek fejlődési egyenleteit nem közvetlenül a kísérletek alapján gondoljuk ki, hanem inkább variációs elvekből vezetjük le. A variációs elvek jelentik tapasztalataink tömörítésének eddig ismert legjobb módját. De a mechanika születésekor kialakult variációs elvekből nem származtathatóak akármilyen fejlődési egyenletek. Tipikusan a disszipatív rendszerekkel van probléma. Ez a probléma nagyjából 150 éves, hiszen már Helmholtz megadta a feltételét, hogy milyen egyenletek származtathatóak variációs elvekből és ezt bizony még a mechanika egyszerű disszipatív egyenletei sem teljesítik, a nemegyensúlyi termodinamika fejlődési törvényei meg pláne nem. Mégha találunk is variációs módszert a hővezetés Fourier-egyenletére, vagy a viszkózus folyadékok Navier–Stokes-egyenletére, az nem olyan, mint az ideális rendszereknél megszokott, csak extra trükkökkel, feltételekkel működik. Az ideális és a valódi, tehát disszipatív világ mintha más elveknek engedelmeskedne.

Körülbelül negyven-ötven éve a nemegyensúlyi termodinamikában a variációs elvek keresésének programja lassan kifulladt. Azért mert új módszerek bukkantak fel. Fentebb említettem a hővezetési egyenlet általánosításait. Ezek levezetésére a legáltalánosabb módszert a nemegyensúlyi termodinamikában találjuk.
A levezetés lényege, hogy minden egyéb feltételt, például az energia megmaradását figyelembe véve olyan egyenletet keressünk, amely biztosítja, hogy az entrópia növekedjen. Tehát a második főtétel, az anyag stabilitásának elve, a fejlődési egyenletek levezetésére is használható (!), természetesen a megfelelő matematikai módszerek segítségével.
Az utóbbi évtizedekben vált világossá, hogy a módszer sokkal szélesebb körben működik, mint eredetileg sejteni lehetett. Pontosabban nincs is egységes módszer, a nemegyensúlyi termodinamika nem egységes, iskolái és csoportjai nem egészen ugyanúgy alkalmazzák a második főtételt. A helyzet most érett meg annyira, hogy ezek a csoportok elkezdtek igen aktívan vitatkozni egymással, elméleti és kísérleti kritériumokat megfogalmazni, matematikai módszereik kritikus elemeit összehasonlítani.
Melyik a jobb elmélet? Mi alapján dönthetünk? Azt gondolnánk, hogy ettől mi sem egyszerűbb, fogalmazzunk meg élesen, vegyünk kísérlettel cáfolhatóan ellenőrizhető követelményeket, vagy vegyük közülük a egyszerűbbet, vagyis alkalmazzuk Ockham borotváját (3. ábra). Csakhogy más-más részterületekre kidolgozott elméletek nehezen összevethetőek egymással, közös jóslatuk is kevés. Másrészt az egyszerűség mint kritérium nem egyszerű, sok esetben eléggé szubjektív, hogy milyen súllyal veszünk figyelembe bizonyos feltételeket. Például egy egyenlet variációs elvekből történő származtathatósága technikailag egyszerűbb a szimmetrikus hiperbolicitás matematikailag tisztább követelményénél.
Egy biztos, egyenleteinket jó lenne egységesen, egyforma elvekből levezetni, ugyanazzal a módszerrel az ideális és a disszipatív rendszerekre. Jelenleg inkább a megkettőzött világkép stratégiája az uralkodó, külön módszerekkel a két területen. A használhatósággal nincs gond, például a fázismező elméletek így működnek. Természetesen ekkor külön kérdés a két világ kompatibilis csatolásának értelmezése, ahogy azt a GENERIC (General Equation for Non-Equilibrium Reversible-Irreversible Coupling) elméletkör teszi, az ideális variációs elveket a második főtétellel párosítva. Ez így egy kettéosztott világra vezet, két független posztulátumcsomaggal. Ockham forog a sírjában. Viszont van egy harmadik út is, ennek az az ára, hogy fel kell tételeznünk, hogy a világ lényegében és alapvetően nem ideális és a tökéletesség az egy kivételes határeset. Ez esetben viszont a második főtételből nem csak a disszipatív, hanem az ideális világnak is származtatni kell az alapvető egyenleteit. Sőt meg kell magyarázni a variációs elveket. Egy termodinamikus számára ez igen rokonszenves stratégia.
Univerzális és abszolút
A nemegyensúlyi termodinamikában dolgozó több kutatási irány az utóbbi években élénkebben kezdett kommunikálni és vitatkozni. Szeretnénk eldönteni melyik a jobb elmélet és pontosan milyen fejlődési egyenletek adódnak termodinamikai módszerekkel. Ebben a vitában fontos állomást jelentenek a szakterület konferenciái, elsősorban a JETC (Joint European Thermodynamics Conference), amely három éve Budapesten zajlott (http://jetc2017.hu/), pont ilyesfajta kérdések megvitatására alkalmas módon szervezve. Fontos lépcsőt jelent továbbá a Philosophical Transactions of Royal Society tavasszal megjelent tematikus különszáma. A nemegyensúlyi termodinamika fundamentális kérdései – Fundamental Aspects of Nonequilibrium Thermodynamics címmel, amelynek célja pontosan a fejlődési egyenletek származtatására vonatkozó stratégiák összevetése volt, az ezen dolgozó irányzatok vezető kutatóinak bevonásával. Ez nem azt jelenti, hogy most már kiderült végre az egyértelmű tudományos igazság. Ez még csak az út eleje. Lényegében annyi történt, hogy az egyes csoportok közötti konstruktív versenyben mindenki kitűzött a többiek számára teljesítendő – itt elsősorban elméleti – célokat. De ez egy konstruktív verseny, tehát a viták mellett közös munkákat is jelent, hiszen egymástól tanulva esetleg gyorsabb és erősebb eredmények születhetnek.
Az egyensúlyi termodinamikában, azaz a termosztatikában a hőmérséklet univerzalitásának bizonyítása azon alapul, hogy általános feltevéseket és fogalmakat használunk. Ilyen elsősorban a második főtétel, illetve a reverzibilis folyamat absztrakciója. Ebből következtetünk arra, hogy a hőmérséklet az anyag szerkezetétől független fizikai mennyiség. Az anyag téridőbeli viselkedését leíró fejlődési egyenleteink a tapasztalaton alapulnak, de általában nem a közvetlen tapasztalaton. Mögöttük általános elvek, természettörvények állnak. Ezek hátterét azonban nem nagyon vizsgáljuk. A természettudományokra kicsit távolabbról ránézve (lásd például [5]) világos, hogy fizika jelenleg a korai természettanhoz hasonlít abból a szempontból, hogy sikeresen osztályozza és részleteiben elemzi a természeti jelenségeket, erőket és kölcsönhatásokat állapít meg. Azaz fajokat és azok közötti rokonságokat állapít meg, részekre szabdalva az egyes egyedeket, de nincs világos képünk arról, hogy van-e ezeknek a törvényeknek közös eredete. Ezen nem sokat segít az sem, hogy a fundamentális dolgokat a mikroszkopikus világ legmélyén keressük, azt gondolva, hogy egy nagy egyesített elméletből majd minden kiderül [6], hiszen a sejtekre bontás sem minden szempontból segít az élet sokféleségének megértésében. A variációs elvekkel elég jól magyarázzuk a világ ideális részét. A nemegyensúlyi termodinamikában most egy új stratégia látszik kibontakozni, amely összekapcsolhatja az elméleti hierarchia szintjeit és egyszerű, egységes alapelvekre alapozhatja a fejlődési törvényeket. Amelyek eredete – a fizikai világban – az
anyag univerzális stabilitása.
A tudomány végtelen és játék
Tehát, ahogy az előbbiekben megpróbáltam érzékeltetni, a nemegyensúlyi termodinamikában különféle stratégiák mentén, részcélok mellett kirajzolódni látszik egy távoli, közös horizont. Ez az a pont, ahol érdemes belegondolni, hogy a tudomány, konkrétabban az elméleti fizika mint szociális, kulturális jelenség micsoda és hogyan működik.
Először is, a tudomány általában információfeldolgozás, a tudósok, kutatóintézetek, egyetemek stb. egy információfeldolgozó gépezetnek az elemei. Ennek a rendszernek két fontos funkciója van. Egyik a tárolás, a másik a tömörítés. A valóságról gyűjtött információink tárolás nélkül elvesznek, tömörítés nélkül használhatatlanok. Mindkét funkcióra számos biológiai, szociális és technikai megoldásunk van. Az emberiség története felfogható e módszerek fejlődési történeteként is. Az információtárolás mostanság bekövetkezett fejlődése ki fogja alakítani az új tömörítési technológiákat. Már érzékelhetőek a változások szociális és intézményi szinteken, a tudományipar forrong.

Ezeket a szociális és intézményi szinteket alulról nézve, az egyén szempontjából, a tudomány egy végtelen csapatjáték. Végtelen játék (lásd [7]), legalábbis emberöltőnél nagyobb távlatban zajlik. Csapatjáték: sokféle, bizonytalan összetételű csapattal. Végső valójában tömörítési játék, mert a gondolat vezérli, az eszmék, az elméletek számítanak. Láthatóvá nehéz tenni, de talán közvetíthető: Bolyai előrevágta a labdát, Einstein lekezelte és fordulásból szöktette a balszélen Hawkingot és lendületben az egyre növekvő csapat, manapság már többezer kutató. De a labda nem is jó metafora, a gondolat sokkal inkább az égen felfénylő szivárvány, amelyhez nézőpont és színlátás kell, ráadásul fel kell emelni a tekintetünk, hogy észrevegyük. A tövében pedig érdemes a kincset keresgélni. Az Einstein által fellőtt általános relativitáselmélet szivárványa felé tudósok nemzedékei indultak el, pár éve néhány ezren, néhány milliárd dollárral kiásták alatta a gravitációshullám-technológiát. Egy másik szivárvány tövében született az internet. Az Erdélyből felívelő geométer-szivárvány olyan hatalmas ívvel, olyan meredeken indult, hogy csak hárman észlelték, és sok évvel Bolyai halála után mutatkozott meg teljes pompájában. A szivárványok követésének végtelen játéka nem verseny (de persze úgy is felfogható) és nincs tétje (de persze pénzben is játszható), a játékért magáért játszák. Sajátossága, hogy kicsit felfelé kell nézni és így az ember könnyen megbotolhat, vagy nekiszaladhat különféle falaknak. Ráadásul addiktív játék, ezért némileg önveszélyes. . Ha ezt így el tudjuk képzelni, akkor az is érthető, hogy egy szivárvány csak bizonyos szögekből látszik és nem mindenkinek ugyanott és nem ugyanúgy ível az égen. Mind az alatta áthaladni akaró megbűvölteknek, mind a tövét kereső kincskeresőknek számolni kell ezzel.
Világos, hogy az ilyen nagy és végtelen játékokban segíthet a végesítés, a kis részekre bontás, konkrét célok kitűzése, csapatok toborozása. Együttműködhetünk a másszivárványosakkal, színtévesztőkkel, a gyengénlátókkal, földet néző kincskeresőkkel, mindenkivel, aki nagyjából ugyanarra tart. Az egész ott kezdődik, amikor felnézünk az égboltra és az ezernyi szivárvány közül kiválasztjuk a legszebbet, esetleg a legnagyobbat vagy a legfényesebbet – a miénket – és aztán elindulunk felé.
Ebből a írásból talán érzékelni lehetett a nemegyensúlyi termodinamika színeit, egy olyan pontból nézve, ahonnan ez a szivárvány gyönyörű, nagyívű, és kirajzolódik az alatta húzódó, színeiben vibráló vidék.
VÁN PÉTER
IRODALOM
[1] T. S. Biró and P. Ván. Zeroth Law compatibility of non-additive thermodynamics. Physical Review E, 83:061147, 2011. arXiv:1102.0536.
[2] Ván P., A. Berezovski, Fülöp T., Gróf Gy., Kovács R., Lovas Á., and Verhás J. Guyer-Krumhansl-type heat conduction at room temperature. EPL, 118:50005, 2017. arXiv:1704.00341.
[3] I. Prigogine and I. Stengers, Az új szövetség (A tudomány metamorfózisa). Akadémiai Kiadó, Budapest, 1995.
[4] T. Matolcsi. Közönséges termodinamika. Scholar Könyvkiadó, 2012.
[5] G. Bogdanov, I. Bogdanov és J. Guitton. Isten és a tudomány. Szent István Társulat, Budapest, 2004.
[6] S. Hossenfelder. Fizikusok útvesztőben. Park, 2020.
[7] J. Carse. Finite and infinite games: A vision of life as play and possibility. New York: Ballantine, 1986.
A cikk a Természet Világa 2020. decemberi számában (151. évf. 12. sz.) jelent meg.


